Konsolidierungsgrad
Inhaltsverzeichnis
1. Grundlagen der Konsolidierung im Baugrund
Bauwerke mit ihren Lasten erzeugen im Boden eine Spannungsveränderung. Um Setzungen im Boden aufgrund dieser Spannungsänderung berechnen zu können, bedarf es der Kenntnis der Ausbreitung und Verteilung der Spannungen im Baugrund. Auf die Möglichkeiten zur Spannungsberechnung wird im Glossareintrag „Setzungsberechnung in der Geotechnik“ eingegangen.
2. Gesamtsetzungen, Konsolidierungssetzungen
Bindige Böden reagieren in Abhängigkeit von der Kornzusammensetzung und dem Wassergehalt mit mehr oder minder zeitlichen verzögerten Setzungen. Die Setzungen in Bodenschichten setzen sich aus drei Anteilen zusammen:
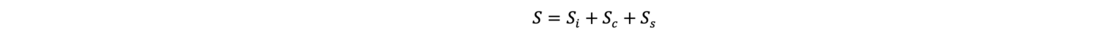
Si sind sofort eintretende Setzungen, die keine Volumenänderungen des Bodens nach sich ziehen. Der Boden weicht unter der Belastung seitlich aus. Oftmals wird auch von einer elastischen Setzung gesprochen.
Sc wird als Konsolidierungssetzung bezeichnet. Sie ist verbunden mit einer Volumenänderung im Boden, das im bindigen Boden befindliche Wasser wird ausgepresst und der Boden nimmt eine dichtere Lagerung an. Wegen der sehr geringen Wasserdurchlässigkeit von bindigen Böden kann sich gleich nach einer Belastung kein Gleichgewicht im Korn-zu-Korn-Druck einstellen, im Zuge des Prozesses des Wasserauspressens wird sich jedoch dieses Gleichgewicht mit der Abnahme des Wassergehalts einstellen. Mit der Zeit wird also der Porenwasserüberdruck, der durch die Belastung entstand, wieder abgebaut. Die Setzungen stellen sich also durch den Abbau des Porenwasserüberdrucks ein. Sc wird auch als primäre Setzung bezeichnet. Bei nichtbindigen Böden treten die Primärsetzungen wegen der hohen Durchlässigkeit zum Zeitpunkt t = 0 auf.
Sekundäre Setzungen Ss entstehen durch Kriechvorgänge im Boden, durch lange andauernde viskose Fließerscheinungen der Kornstruktur bedingte Setzungen. Im Zeit-Setzungs-Diagramm erkennt man die sekundären Setzungen durch stetiges Wachsen nach den primären Setzungen. Die Zeit-Setzungs-Linie nähert sich also nicht asymptotisch einer Horizontalen an.
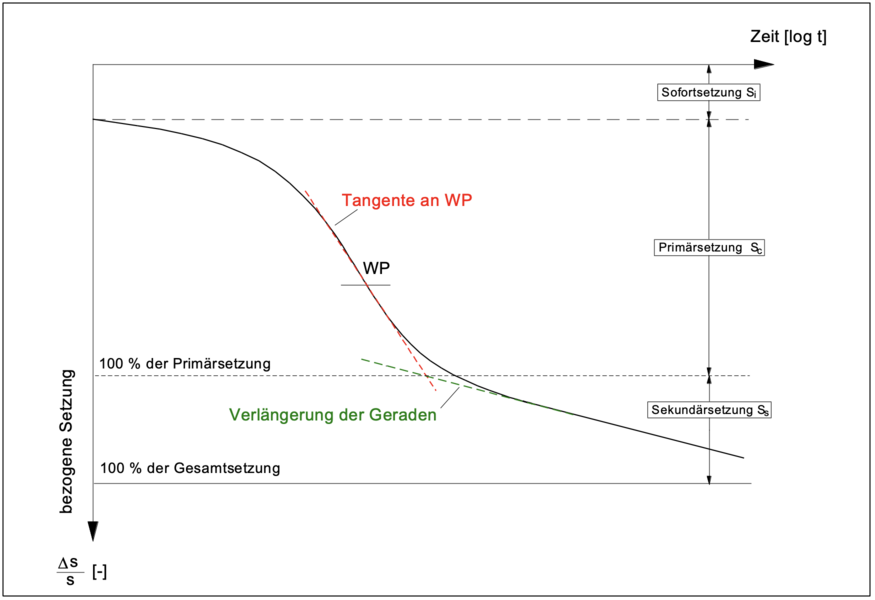
Nach einer Sofortsetzung (t = 0) beginnt der Konsolidierungsprozess, die Konsolidierungssetzungen wachsen an. Die Grenze zwischen Primär- und Sekundärsetzung ergibt sich im logarithmischen Maßstab aus dem Schnittpunkt der Tangente an den Wendepunt der Zeit-Setzungslinie im Primärsetzungsbereich und der Verlängerung der Geraden, die die Sekundärsetzungen beschriebt.
Die Differentialgleichung, die einen eindimensionalen Konsolidierungsvorgang beschreibt, lautet nach Terzaghi (1923):
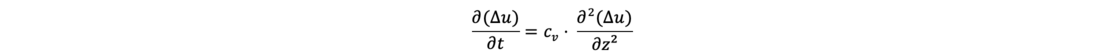
Diese Gleichung ist eine partielle lineare und homogene Differentialgleichung 2. Ordnung. Auf die Lösung der Dgl. wird im Glossareintrag „Eindimensionale Konsolidierungstheorie“ eingegangen.
3. Konsolidierungsgrad Bedeutung
Die Primärsetzung eines bindigen Bodens s(t) ergibt sich aus dem Volumen des ausgepressten Wassers. Sie strebt einem Grenzwert (Maximalwert = Endsetzung) entgegen s(t = ∞). Deren Verhältnis wird als Konsolidierungsgrad uK bezeichnet.
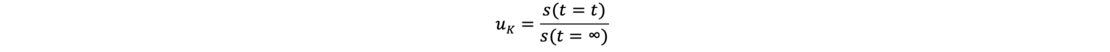
Als setzungserzeugende Spannung in einer Bodenschicht zu einer Zeit t wirkt die effektive Spannung σ‘. Die neutrale Spannung u zum Zeitpunkt t setzt sich aus dem hydrostatischen Wasserdruck u0 und dem Porenwasserüberdruck Δu zusammen, wobei für die Konsolidierungstheorie nur der Porenwasserüberdruck Δu entscheidend ist. Somit gilt für die Konsolidierungsberechnungen
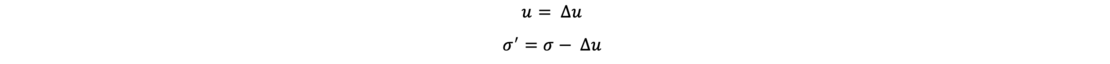
Durch Integration der setzungserzeugenden – effektiven - Spannungen, dividiert durch den Steifemodul erhält man die Setzung einer Bodenschicht. Die Endsetzung kann ermittelt werden:
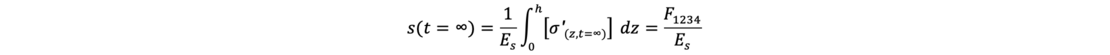
Für einen betrachteten Zeitpunkt t können die effektiven Spannungen mit
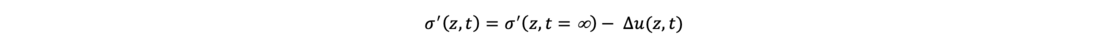
bestimmt werden. Die zugehörigen Setzungen sind
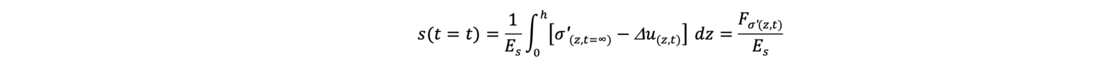
Der Konsolidierungsgrad uk ergibt sich somit zu
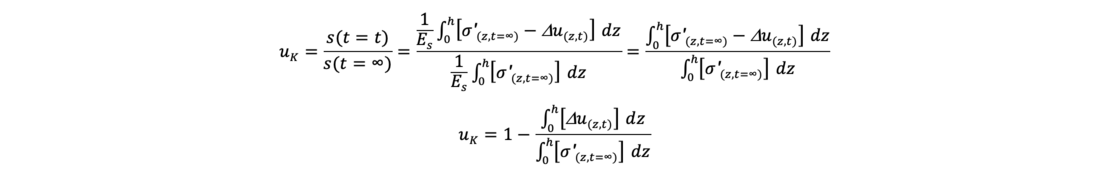
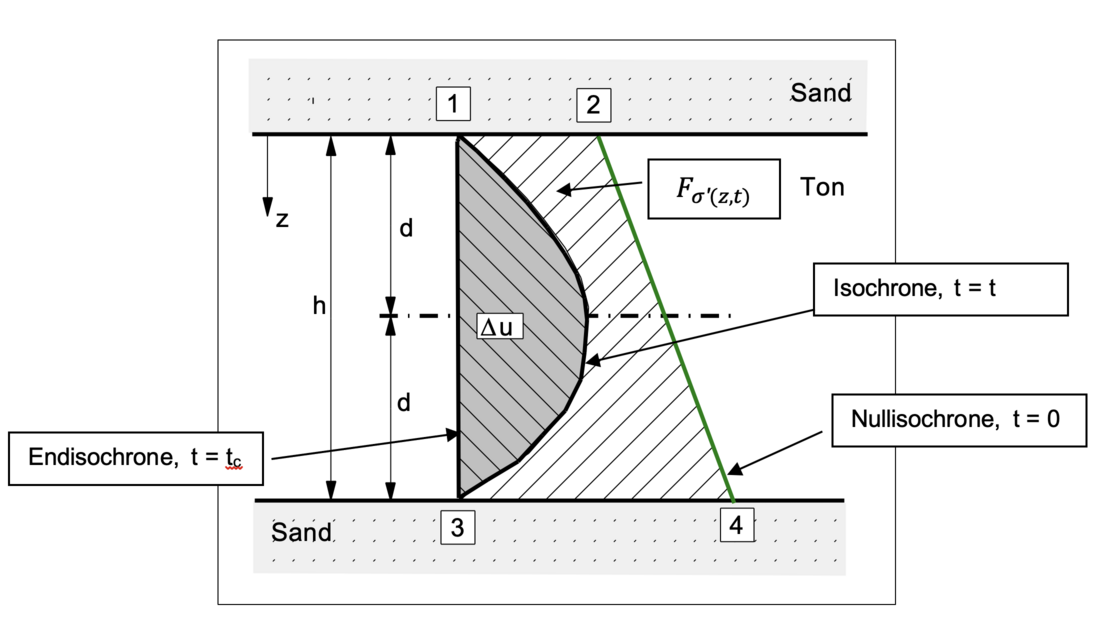
Anschaulich ist der Konsolidierungsgrad uK das Verhältnis der schraffierten Fläche Fσ‘(z,t) (= effektive Spannungen zur Zeit t) zur Gesamtlastfläche F1234 als wirksame Spannung zur Zeit t = ∞. Exemplarisch wird hier die Verteilung von effektiven Spannungen und Porenwasserüberdruck für eine zu entwässernde Tonschicht mit zwei offenen Rändern aus Sand gezeigt.
Der Konsolidierungsgrad Uk kann in Abhängigkeit von der Zeit t für eine zweiseitige Entwässerung bei linearer Nullisochrone berechnet werden mit T als dimensionslosem Zeitfaktor (Steifemodul Es, Durchlässigkeit kf, Wichte des Wassers yw):
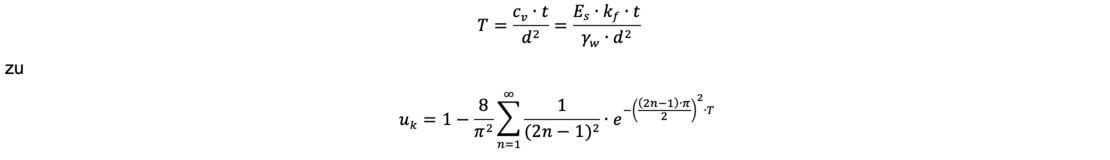
und für eine einseitige Entwässerung mit
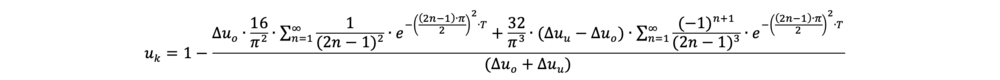
Für unterschiedliche Anfangsbedingungen, die mit der Nullisochrone beschrieben werden, lässt sich die obige Gleichung vereinfachen:
Δuo = Δuu: konstante Porenwasserdruckverteilung über die zu entwässernde Bodenschicht
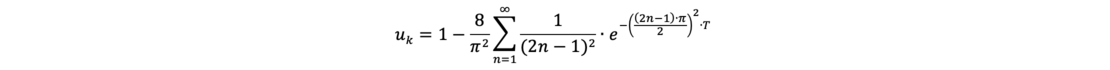
Δuo = 0: linear mit der Tiefe ansteigende Porenwasserdruckverteilung über die zu entwässernde Bodenschicht
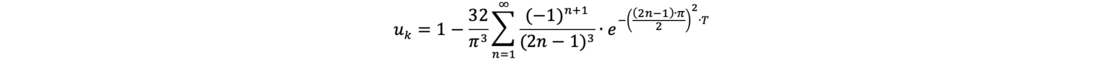
Δuu = 0: linear mit der Tiefe, auf Null abnehmender Porenwasserdruck über die zu entwässernde Bodenschicht
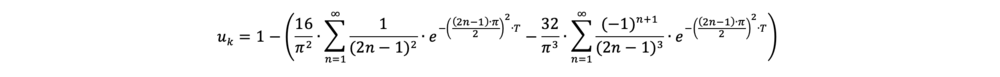
4. Beispiel Konsolidierungsberechnung, Video zu GGU-CONSOLIDATE
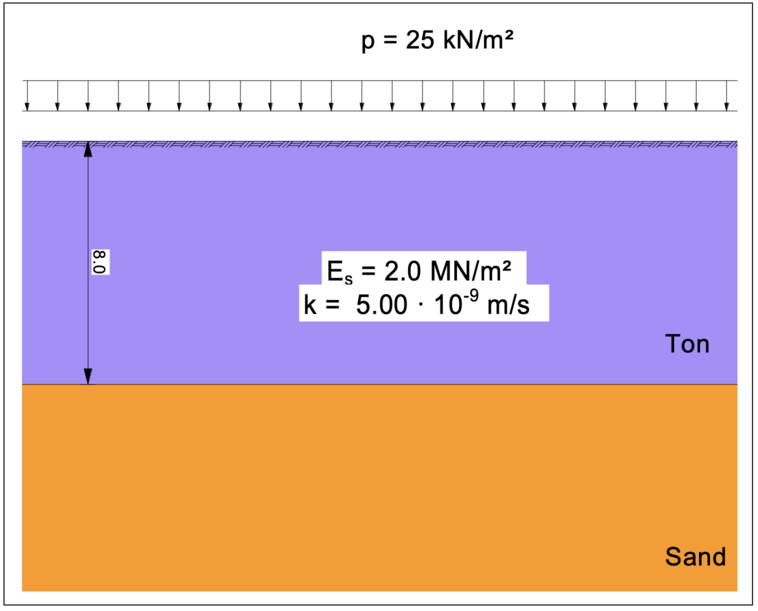
Für das unten gezeigte Beispiel einer 8 m dicken Tonschicht, die mit einer unbegrenzten Flächenlast von p = 25 kN/m² belastet wird, soll gemäß der eindimensionalen Konsolidierungstheorie mit Hilfe des Programms GGU-CONSOLIDATE der Zeitpunkt für einen Konsolidierungsgrad von Uk = 85 % und die dazugehörige Setzung der Geländeoberkante bestimmt werden.
Hinweise zur Nutzung
Alle hier aufgeführten Texte, Bilder und Medien unterliegen dem Urheberrecht und sind geistiges Eigentum der Civilserve GmbH. Verwendung ist nur mit entsprechendem Hinweis und einer Verlinkung auf diese Quelle erlaubt.