Setzungsberechnung in der Geotechnik
Inhaltsverzeichnis
1. Spannungsberechnung
Bauwerke mit ihren Lasten erzeugen im Boden eine Spannungsveränderung. Um Setzungen im Boden aufgrund dieser Spannungsänderung berechnen zu können, bedarf es der Kenntnis der Ausbreitung und Verteilung der Spannungen im Baugrund.
Die Spannungen werden an einem elastisch-isotropen Halbraum berechnet. Der dreidimensionale Raum wird durch eine waagerechte, unendlich ausgedehnte Ebene in zwei Hälften unterteilt. Der obere Teil ist leer, der untere mit einem homogenen Stoff gefüllt, der sich elastisch verhält. Durch einen doppelten senkrechten Schnitt wird die aus diesem Halbraum eine Halbscheibe herausgeschnitten, die zur Lösung sämtlicher ebener Probleme herangezogen wird.
Der Halbraum besitzt die folgenden Eigenschaften:
- das Eigengewicht des Halbraums wird nicht berücksichtigt,
- der Halbraum ist homogen, Elastizitätsmodul E und Querdehnzahl (Poissonzahl) v sind in einer Richtung innerhalb des Halbraum überall gleich,
- der Halbraum ist isotrop, die mechanischen Eigenschaften E und ν sind in allen Richtungen gleich,
- der Halbraum ist elastisch, das Hooke’sche Gesetz gilt. Spannungsanteile können linear überlagert werden
1.1 Spannungsverteilung im Boden
Die Spannungen im Untergrund infolge der Lasten eines Bauwerks breiten sich mit wachsender Tiefe aus. Es zeigt sich, dass sie unter der Mitte des Bauwerks größer sind, als zu den Seiten hin. Analytische Lösungen für unterschiedliche Lasten für den elastischen, isotropen Halbraum stehen zur Verfügung. Dabei werden von unterschiedlichen Autoren Einflusswerte i zur Berechnung der Spannungen im Baugrund in Abhängigkeit von der Größe des Lasteintrags, der betrachteten Tiefe und dem Abstand zum Lasteintrag in tabellarischer Form angegeben.
Bei weiteren Betrachtungen muss noch unterschieden werden zwischen Lasten aus starren und schlaffen Fundamenten.
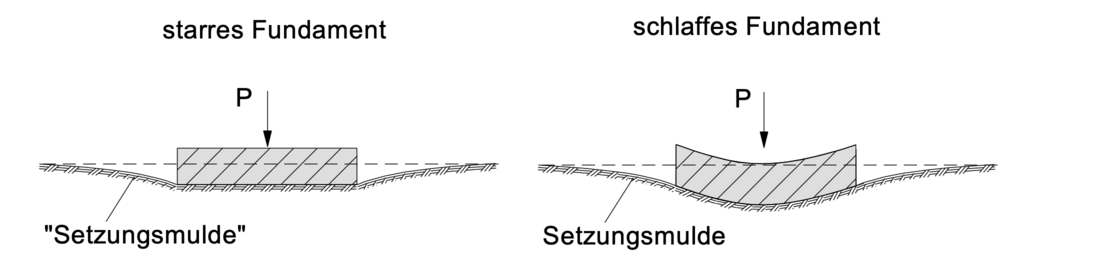
Ein schlaffes Fundament beschreibt zusammen mit dem anstehenden, belasteten Boden eine gemeinsame Setzungsmulde. Die Sohlspannungsverteilung ist bekannt und entspricht der darüber stehenden Belastung (z.B. aufgeschütteter Erddamm, frisch gegossener Beton).
Bei starren Fundamenten ist die vertikale Verschiebung des Fundaments in den Baugrund hinein an jeder Stelle des Fundaments gleich. Es kann sich keine Setzungsmulde mehr ausbilden. Die vertikalen Spannungen müssen daher zum Rand hinzunehmen. Theoretisch treten dort Spannungsspitzen auf, die jedoch auf das Niveau von dem Boden zulässigen Grenzspannungen korrigiert werden.
1.2 Lösung für verschiedene Lasten
Analytische Lösungen für unterschiedliche Lasten werden u. a. im Baugrundtaschenbuch gegeben. Hierzu gehören u.a. Lösungen für senkreche und waagerechte Lasten, Punkt, Linien und Flächenlasten. Es werden in tabellarischer Form bzw. mit Gleichungen Einflusswerte i gegeben, mit denen Spannungen im Boden in unterschiedlichen Tiefen und Abständen zum Lasteintrag berechnet werden können. Autoren dieser Tabellen sind u.a. Terzaghi, Jelinek, Gilboy, Newmark, Boussinesq, Kany und Steinbrenner.
Häufige Anwendung findet die Lösung nach Steinbrenner. Es kann die setzungserzeugende Spannung σz in einer Tiefe z für eine gleichförmige schlaffe Flächenlast unter einem Eckpunkt dieser Flächenlast mit den Dimensionen a und b bestimmt werden zu:
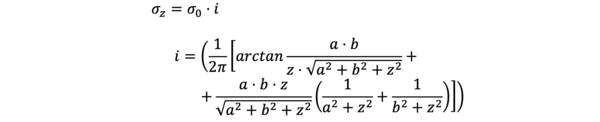
Die Spannung σz,P unter einem beliebigen Punkt P innerhalb bzw. außerhalb der Lastfläche wird berechnet, indem die belastete Grundfläche so in Teilrechtecke zerlegt wird, dass der betrachtete Punkt jeweils der Eckpunkt von den angrenzenden Teilrechtecken ist. Die Spannungsanteile der Teilrechtecke werden dann superponiert. So wird bei einer Belastung des Baugrunds mit einer gleichmäßig verteilten Spannung σ0 die Spannung σz,P unterhalb des Punkts P innerhalb der Belastungsfläche bzw. außerhalb der Belastungsfläche mit den folgenden Superpositionsvorschriften ermittelt:
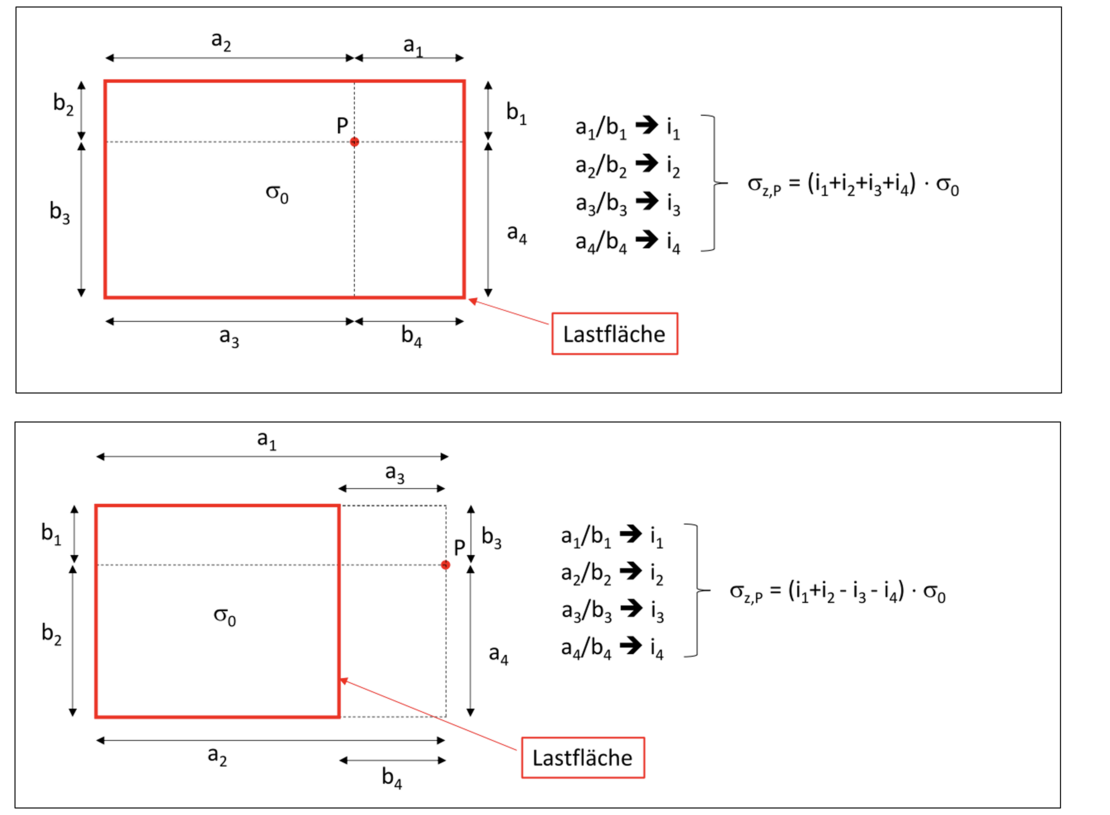
Weitere Beispiele zur Lösungsstrategie im Zuge der Ermittlung von Spannungen an verschiedensten Orten für Belastungsflächen mit unterschiedlichsten Geometrien finden Sie im Themenbereich „Setzungsberechnung, Spannungen nach Steinbrenner“.
1.3 Spannungen unterhalb eines starren Fundaments
Die Orte, an denen die Verformungen eines schlaffen und starren Fundaments gleich sind, werden als „kennzeichnende Punkte“ bezeichnet. Die Setzungen starrer Fundamente können daher bei Kenntnis der Spannungen σz,K in der Tiefe z unter dem kennzeichnenden Punkt auch mit Hilfe der Berechnungen für schlaffe Fundamente bestimmt werden.
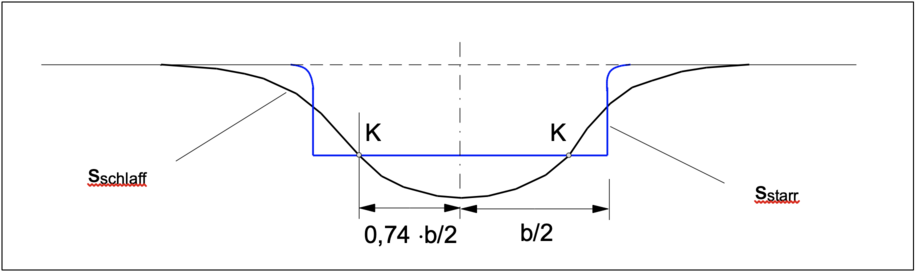
Beim Rechteck liegt der kennzeichnende Punkt K bei 0,74 · a/2 bzw. 0,74 · b/2, beim Kreis im Abstand von 0,845 · r vom Mittelpunkt.
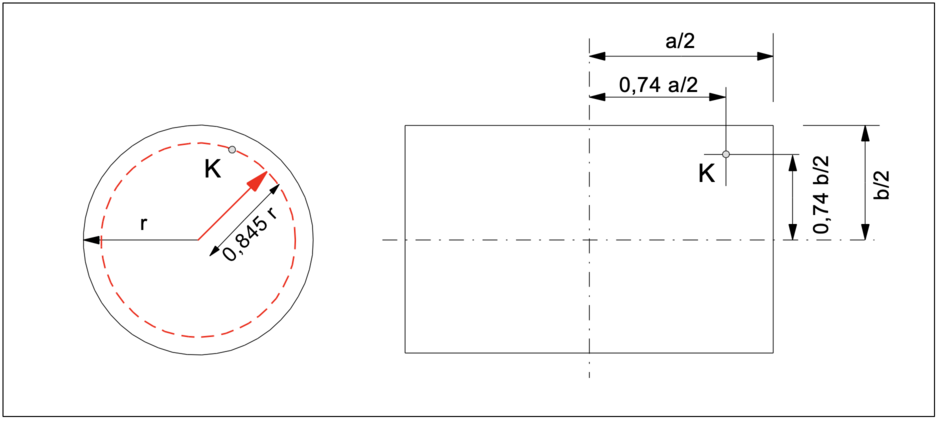
Zur Berechnung der Spannungen unterhalb des kennzeichnenden Punkts stehen Einflusswerte i nach Kany zur Verfügung. Eine Unterteilung der Gesamtlastfläche in Teilrechtecke ist in den Einflusswerten bereits berücksichtigt.
2. Setzungsberechnung
2.1 Setzungsberechnung mit Hilfe von vertikalen Spannungen
Die Setzung s infolge einer Belastung des Bodens kann als Integral der Dehnungen ε über die Tiefe z mit der folgenden Gleichung berechnet werden:
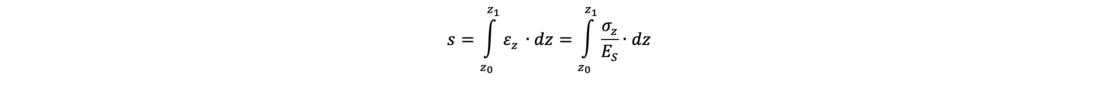
Zur Bestimmung der Setzungen innerhalb der einzelnen Teilschichten müssen daher bekannt sein:
- Verlauf der Vertikalspannungen σz. Bei den Setzungsberechnungen ist bei in das Erdreich eingebundenen Fundamenten die um die Aushubentlastung reduzierte setzungserzeugende Sohlspannung σ1 = σ0 - γ * h anzusetzen.
- spannungsabhängige Steifemoduli der Böden
- Grenztiefe der Setzungsermittlung
Für eine näherungsweise Berechnung der Setzungen wird die Spannungsverteilung in zu betrachtende Teilschichten, sogenannte Lamellen, mit der Dicke Δzi unterteilt. Für eine gute Näherungslösung ist anzustreben, dass in diesen Teilschichten der Spannungsverlauf annähernd linear verläuft. In jeder einzelnen Lamelle resultiert aus der Auflast eine Spannungserhöhung. Zur Berechnung der Setzungsanteile werden die mittleren, konstanten Spannungen σkonst,i für alle i Lamellen ermittelt. Die Gesamtsetzung ist gleich der Summe der Teilsetzungen aller Lamellen. Nachfolgend ist ein Beispiel mit 6 Lamellen dargestellt.
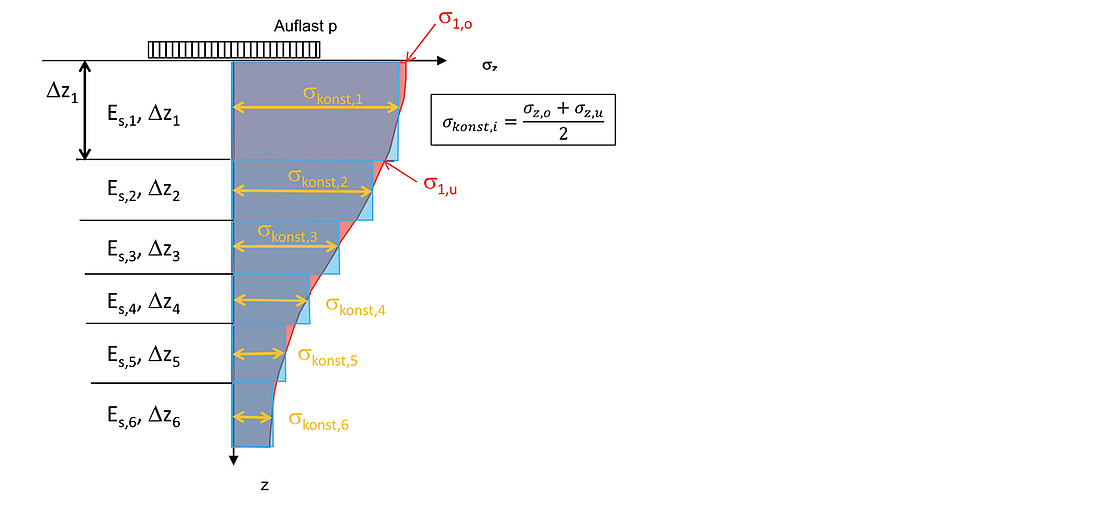
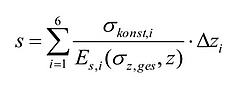
2.2 Setzungsberechnung mit Hilfe von geschlossenen Formeln
Das Verfahren zur Berechnung der Setzungen s infolge der Spannung σ0 beruht auf Erfahrungswerten für den mittleren Steifemodul Em und der Gleichung
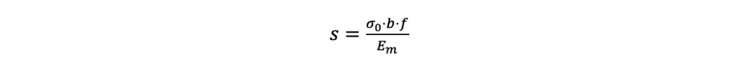
Der Term σ0 · b · f steht dabei für das Integral der Spannungsfläche bis zur Grenztiefe. Die DIN 4019 verweist auf Tafeln zur Bestimmung dieses Setzungsbeiwerts f nach Kany. Diese Tabelle ist für ungeschichteten Boden mit einem mittleren Steifemodul anwendbar. Sollen mit dieser Methode die Setzungen in einem geschichteten Baugrund berechnet werden, werden für jede einzelne Schicht Setzungsbeiwerte bestimmt, die Setzungsanteile der einzelnen Schichten ergeben sich aus der Differenz der Setzungsbeiwerte:
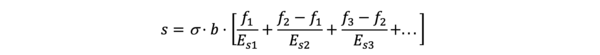
2.3 Grenztiefe
DIN 4019 begrenzt die Mächtigkeit der zusammendrückbaren Schicht in einer Tiefe, in der die setzungserzeugenden Spannungen kleiner als 20 % der Überlagerungsspannungen σü werden. Diese Tiefe wird mit der Grenztiefe bezeichnet, tGrenz.
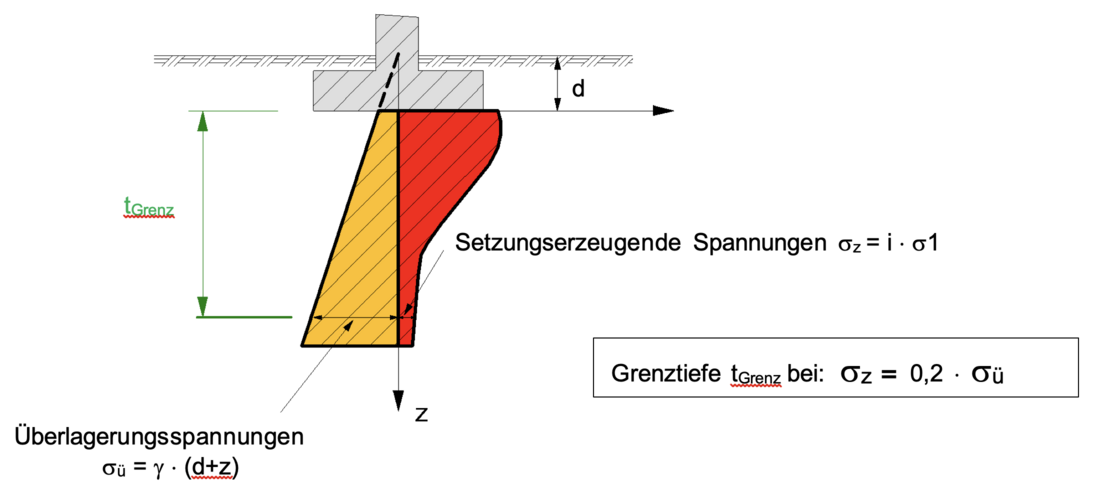
Über diese Grenztiefe hinaus werden keine Setzungsanteile mehr berücksichtigt, es sei denn, es stehen z. B. stark setzungsempfindliche Bodenschichten unterhalb der Grenztiefe an, die noch einen signifikanten Beitrag zur Gesamtsetzung leisten.
3. Konsolidierungssetzungen
In den vorhergehenden Kapiteln wurde die Berechnung von Endsetzungen vorgestellt. Bindige Böden reagieren jedoch in Abhängigkeit von der Kornzusammensetzung und dem Wassergehalt mit mehr oder minder zeitlichen verzögerten Setzungen. Die Setzungen in Bodenschichten setzen sich aus drei Anteilen zusammen:
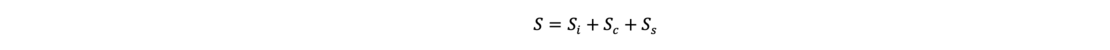
Si sind sofort eintretende Setzungen, die keine Volumenänderungen des Bodens nach sich ziehen. Der Boden weicht unter der Belastung seitlich aus. Oftmals wird auch von einer elastischen Setzung gesprochen.
Sc wird als Konsolidierungssetzung bezeichnet. Sie ist verbunden mit einer Volumenänderung im Boden, das im bindigen Boden befindliche Wasser wird ausgepresst und der Boden nimmt eine dichtere Lagerung an. Wegen der sehr geringen Wasserdurchlässigkeit von bindigen Böden kann sich gleich nach einer Belastung kein Gleichgewicht im Korn-zu-Korn-Druck einstellen, im Zuge des Prozesses des Wasserauspressens wird sich jedoch dieses Gleichgewicht mit der Abnahme des Wassergehalts einstellen. Mit der Zeit wird also der Porenwasserüberdruck, der durch die Belastung entsteht, wieder abgebaut. Die Setzungen stellen sich also durch den Abbau des Porenwasserüberdrucks ein. Sc wird auch als primäre Setzung bezeichnet. Bei nichtbindigen Böden treten die Primärsetzungen wegen der hohen Durchlässigkeit zum Zeitpunkt t = 0 auf.
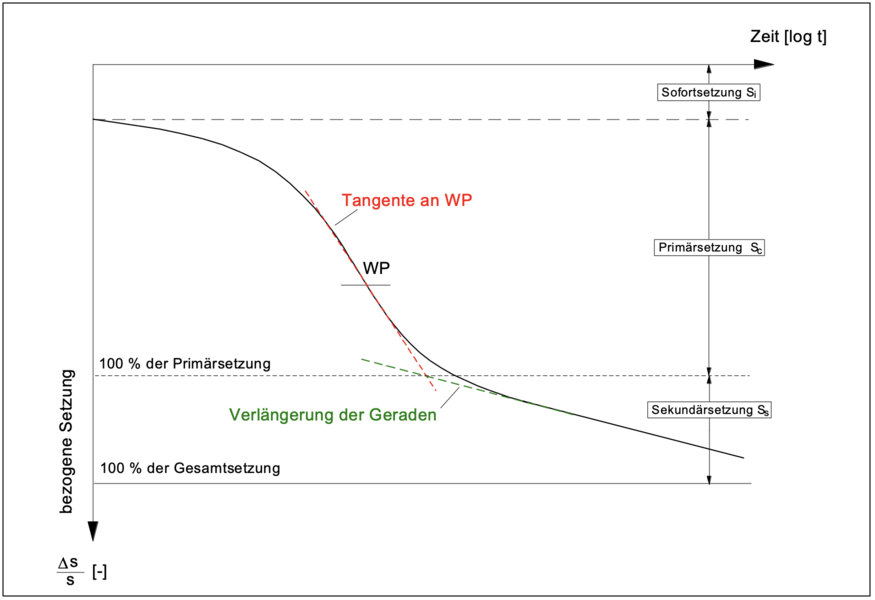
Sekundäre Setzungen Ss entstehen durch Kriechvorgänge im Boden, durch lange andauernde viskose Fließerscheinungen der Kornstruktur bedingte Setzungen. Im Zeit-Setzungs-Diagramm erkennt man die sekundären Setzungen durch stetiges Wachsen nach den primären Setzungen. Die Zeit-Setzungs-Linie nähert sich also nicht asymptotisch einer Horizontalen an.
Unmittelbar nach einer Sofortsetzung Si (t = 0) beginnt der Konsolidierungsprozess, die Konsolidierungssetzungen wachsen an. Die Grenze zwischen Primär- und Sekundärsetzung ergibt sich im logarithmischen Maßstab aus dem Schnittpunkt der Tangente an den Wendepunt der Zeit-Setzungslinie im Primärsetzungsbereich und der Verlängerung der Geraden, die die Sekundärsetzungen beschriebt.
Die Differentialgleichung, die einen eindimensionalen Konsolidierungsvorgang beschreibt, lautet nach Terzaghi (1923):
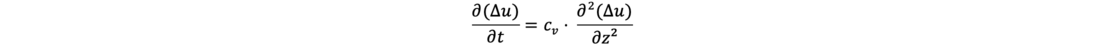
Diese Gleichung ist eine partielle lineare und homogene Differentialgleichung 2. Ordnung. Der Term cv ist dabei der sogenannte Verfestigungsbeiwert. Mit der Durchlässigkeit kf, der Wichte des Wassers γw und dem Steifemodul Es ergibt er sich zu:
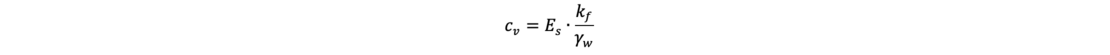
Zur Lösung dieser Dgl. wird ein Produktansatz nach Bernoulli verwendet, wobei φ(t) eine nur von der Zeit und ψ(z) eine nur von der Tiefe abhängige Funktion darstellt.
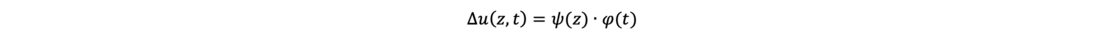
Dadurch wird die partielle Dgl. in zwei gewöhnliche Dgls. aufgespalten. Zur Lösung wird eine Anfangsbedingung (Nullisochrone) und zwei homogene Randbedingungen (Entwässerungsbedingungen) benötigt. Nach einigen Umformungen ergeben sich zwei gewöhnliche Differentialgleichungen
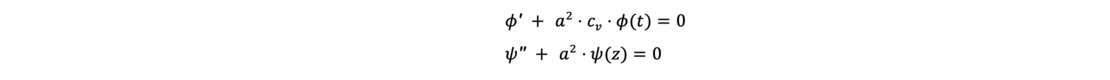
die die folgenden Lösungen besitzen:
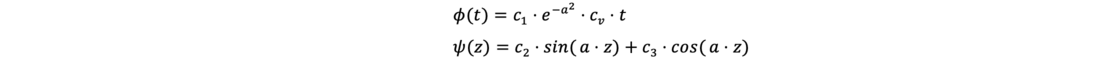
Zur Lösung müssen die Entwässerungs-Randbedingungen in diese Gleichungen eingearbeitet werden, damit die Konstanten C1 bis C3 bestimmt werden können. Mit den daraus resultierenden Gleichungen für den Porenwasserüberdruck Δu in Abhängigkeit von der Zeit und der Tiefe z können Isochronen für verschiedene Anfangs- und Randbedingungen berechnet werden. Sie stehen als Graphiken in vielen Standardwerken zur Verfügung.
3.1 Konsolidierungsgrad
Die Primärsetzungsanteile eines bindigen Bodens s(t) ergeben sich aus dem Volumen des ausgepressten Wassers. Sie streben einem Grenzwert (Maximalwert = Endsetzung) entgegen s(t = ∞). Deren Verhältnis wird als Konsolidierungsgrad uK bezeichnet.
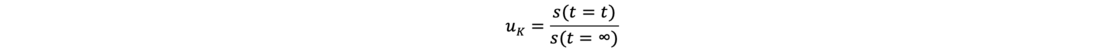
mit
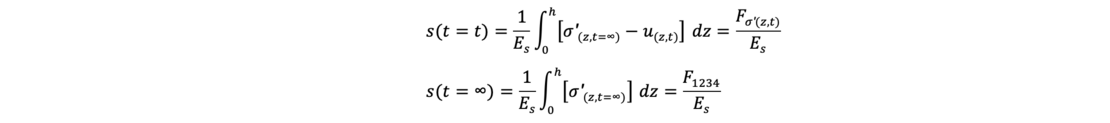
wird
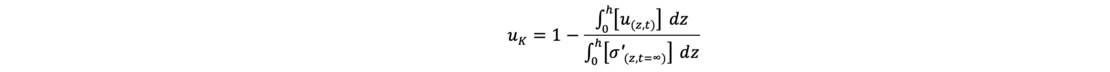
Anschaulich ist der Konsolidierungsgrad uK das Verhältnis der schraffierten Fläche (= wirksame Spannungen) zur Zeit t zur Gesamtlastfläche 1234 als wirksame Spannung zur Zeit t = ∞. Exemplarisch wird hier eine zu entwässernde Tonschicht mit zwei offenen Rändern aus Sand gezeigt.
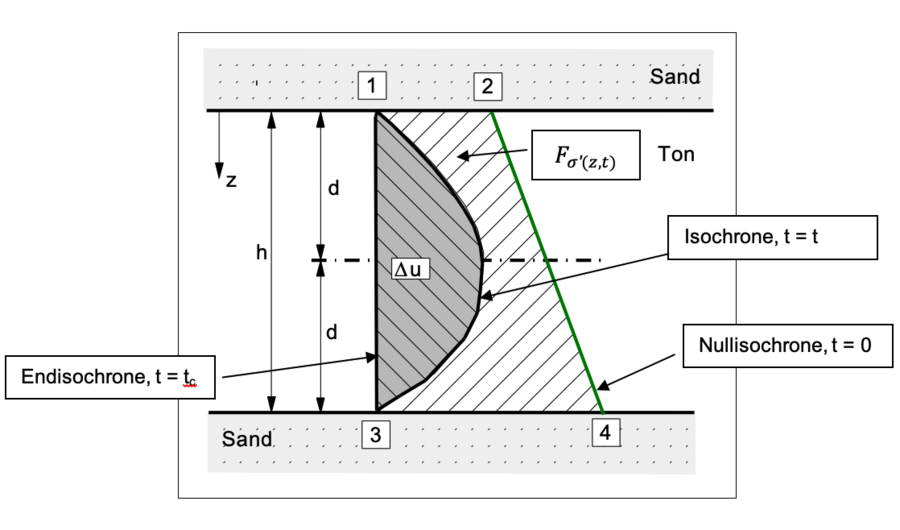
4. Beispiel Setzungsberechnung, Video zu GGU-SETTLE
Für das unten gezeigte Beispiel einer 100 m langen und 35 m breiten Aufschüttung (Damm) mit einer Höhe von 5 m auf dem gewachsenen Gelände wird im nachfolgenden Video gezeigt, wie mit dem Programm GGU-SETTLE die Setzungsberechnung durchgeführt werden kann. Es wird für dieses Beispiel vereinfachen angenommen, dass sich die dargestellte Bodenschichtung entlang der Längsachse des Damms nicht verändert.
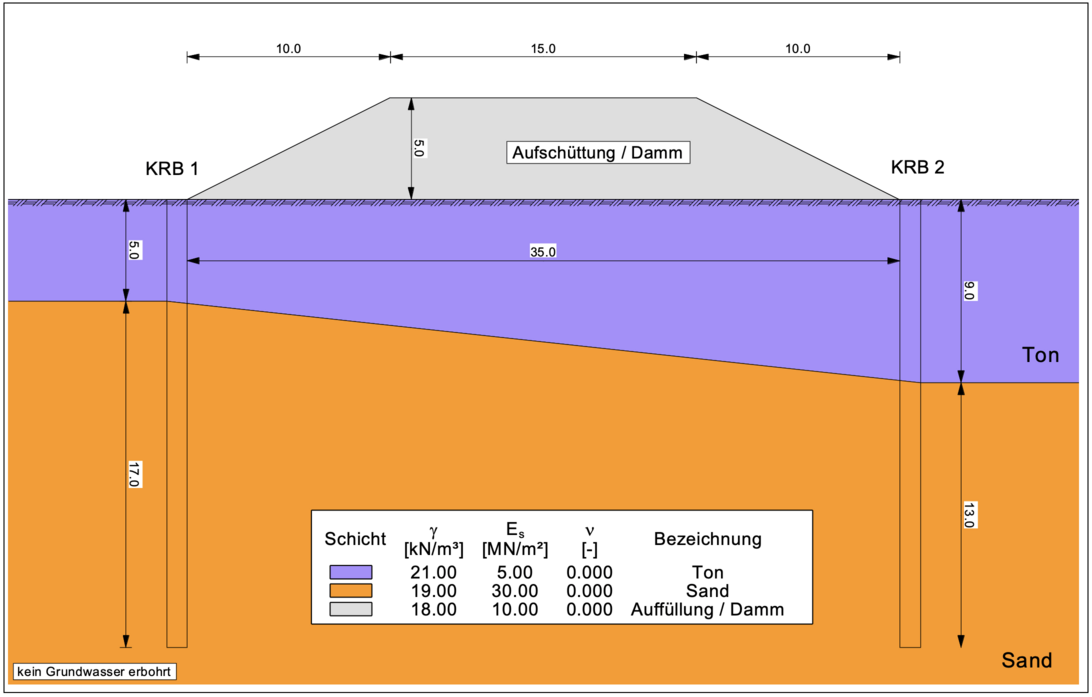
5. Beispiel Konsolidierungsberechnung, Video zu GGU-CONSOLIDATE
Für das unten gezeigte Beispiel einer 8 m dicken Tonschicht, die mit einer unbegrenzten Flächenlast von p = 25 kN/m² belastet wird, soll gemäß der eindimensionalen Konsolidierungstheorie mit Hilfe des Programms GGU-CONSOLIDATE der Zeitpunkt für einen Konsolidierungsgrad von Uk = 85 % und die dazugehörige Setzung der Geländeoberkante bestimmt werden.
Hinweise zur Nutzung
Alle hier aufgeführten Texte, Bilder und Medien unterliegen dem Urheberrecht und sind geistiges Eigentum der Civilserve GmbH. Verwendung ist nur mit entsprechendem Hinweis und einer Verlinkung auf diese Quelle erlaubt.