Setzungsberechnung einer Bodenplatte mit dem Bettungsmodulverfahren

Das Bettungsmodulverfahren beschreibt ein linear-elastisches Spannungs-Verformungsverhalten des Bodens. Das auf dem Boden liegende biegesteife Fundament wird mit Federn gebettet, die den nachgiebigen Boden repräsentieren. Das Verfahren beruht auf der Winkler’schen Hypothese, die eine lineare Beziehung zwischen dem Baugrund und der Sohlpressung zugrunde legt.

Der Baugrund wird durch einzelne, voneinander entkoppelte Federn ersetzt:

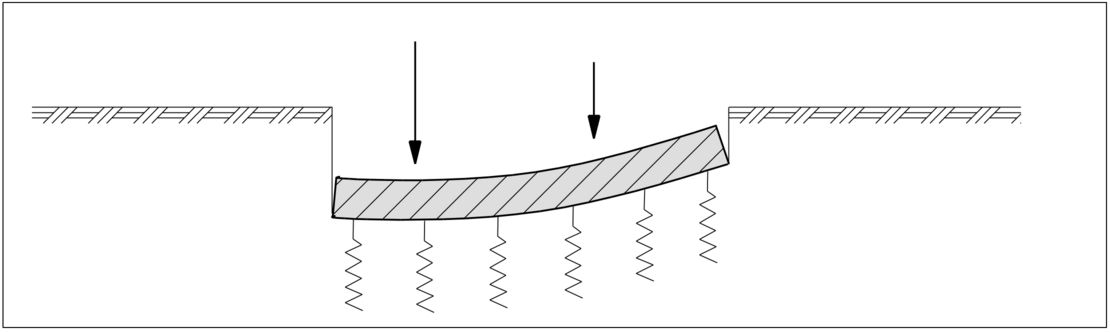
Jede Feder wird durch den auf ihr lastenden Sohldruck belastet bzw. zusammengedrückt. Es wird keine Schubfestigkeit angenommen, so dass der Einfluss benachbarter Sohldrücke nicht berücksichtigt wird. Die Mitwirkung des umgebenden Bodens wird mit diesem Verfahren nicht erfasst.

Das Bettungsmodulverfahrens ist für Systeme anwendbar, bei denen eine weitreichende Beteiligung des umliegenden Bodens nicht zu erwarten ist, oder die eine große Längenausdehnung besitzen, so dass eine Aktivierung der Schubsteifigkeit keine Rolle spielt, z.B. bei langen Straßen, bei Landebahnen o. dgl.. Sollen Setzungen von nah aneinander gelegenen Einzelfundamenten berechnet werden, ist das Verfahren weniger geeignet, da die Schubsteifigkeit und die gegenseitige Beeinflussung der einzelnen Fundamente nicht berücksichtigt wird.

Der Bettungsmodul k_s beschreibt das Verhältnis zwischen der Sohlpressung σ und der daraus resultierenden Setzung s des Bodens:

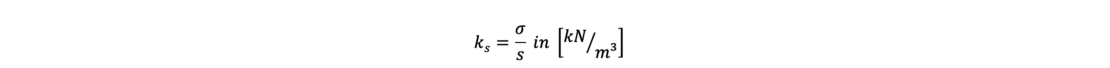
Eine gleichmäßige Belastung führt bei gleichen Werten für den Bettungsmodul über die betrachtete Gründungsfläche nicht zu einer Setzungsmulde, sondern zu einer gleichmäßigen Setzung eines – an jeder Stelle gleich dicken – Fundaments. Dies resultiert in einem Sprung in der Setzungslinie an den Rändern des Fundaments, vgl. Bild oben. Dieser verdeutlicht, dass eine Schubsteifigkeit des Bodens nicht berücksichtigt wird.

Es ist wichtig zu verstehen, dass der Bettungsmodul keine Bodenkonstante bzw. keine reine Bodeneigenschaft ist, sondern von der Steifigkeit des Bauwerks und der Verteilung von Steifigkeiten auf der Sohlfläche abhängig ist. Selbst für gleiche Bodeneigenschaften im Bereich einer Gründungsfläche sind im Allgemeinen unterschiedliche Bettungsmoduli anzusetzen.  Der Bettungsmodul ist für eine Gründungsfläche nicht konstant!

Die folgende Differentialgleichung beschreibt das Problem einer gebetteten Biegeplatte und wird zumeist numerisch gelöst:

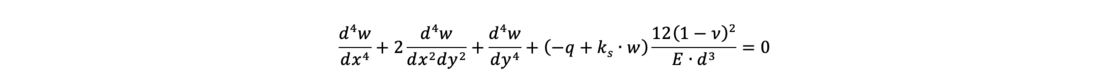
Dabei sind

• w:        Durchbiegung der Platte [m]
• d:         Dicke der Platte [m]
• E:        Elastizitätsmodul der Platte [kN/m²]
• ν:         Querkontraktionszahl des Betons [-]
• k_s:        Bettungsmodul [kN/m³]
• q:         Flächenlast [kN/m²]

Das Programm GGU-SLAB berücksichtigt die Steifigkeit der Fundamentplatte und weiterer Gebäudeteile (z.B. Wände, Unterzüge o. dgl.) zur Ermittlung von Zustandsgrößen und der Durchbiegung der Fundamentplatte auch nach dem Bettungsmodulverfahren. Nach der Definition eines FE-Netzes können entlang von Knoten des FE-Netzes Stäbe definiert werden, die bei der späteren Plattenberechnung hinsichtlich ihrer Steifigkeit berücksichtigt werden. Das ist z.B. sinnvoll, wenn der Einfluss von Fundamentbalken, Wänden, Unterzügen o.ä. berücksichtigt werden soll. Grundsätzlich kann ein Fundamentbalken auch über eine Verdickung der Platte in entsprechenden Bereichen modelliert werden.

Auch mit dem Programm GGU-SETTLE, das die Berücksichtigung einer Plattensteifigkeit nicht vorsieht, können Systemsteifigkeiten berücksichtigt werden.

Dies erfordert eine iterative Lösungsstrategie mit einem Zusammenarbeiten von Baugrundgutachter und Tragwerksplaner:

In einem ersten Iterationsschritt wird (vom Tragwerksplaner) die Berechnung für einen gebettetes System durchgeführt, das die Systemsteifigkeiten berücksichtigt. Hierfür wird eine sinnvolle Verteilung des Bettungsmoduls über die Gründungsfläche angenommen. Dies resultiert in einer - aufgrund der Systemsteifigkeiten über die Gründungsfläche variierenden – Sohldruckverteilung. Diese Sohldruckverteilung wird als Belastung in einer Setzungsberechnung (vom Baugrundgutachter) angesetzt. Dies wiederum erbringt eine veränderte Verteilung von Bettungsmoduli unterhalb der Sohlfläche, die im nächsten Iterationsschritt im System des Tragwerksplaners berücksichtigt wird und nochmals veränderte Sohlpressungen erbringt.

Weichen die berechneten Werte für die Sohlpressungen von zwei aufeinander folgenden Iterationsschritten nicht mehr signifikant voneinander ab, kann die Iteration beendet werden.

Zur allgemeinen Handhabung dieses Programms werden im Glossareintrag „Setzungsberechnung in der Geotechnik“ Hinweise gegeben.

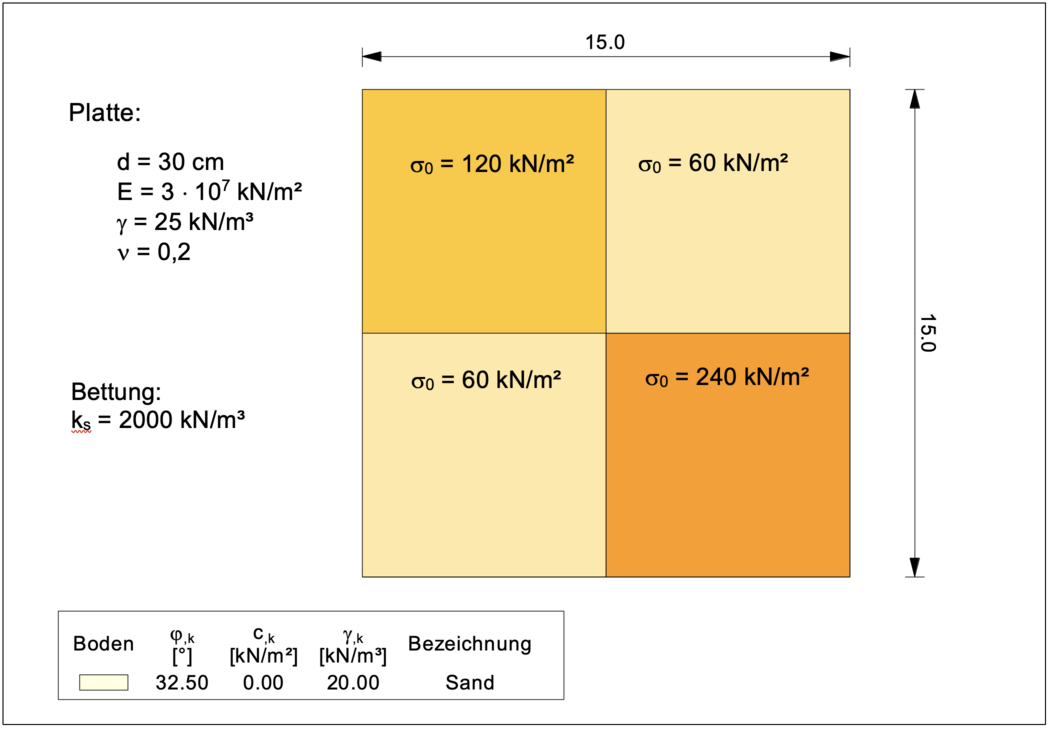
Für das unten gezeigte Beispiel einer 30 cm dicken Fundamentplatte mit ungleichmäßiger Belastung zwischen σ₀ = 60 kN/m² und σ₀ = 240 kN/m² wird im nachfolgenden Video gezeigt, wie mit dem Programm GGU-SLAB eine Setzungsberechnung mit Bemessung der Stahlbetonplatte nach dem Bettungsmodulverfahren durchgeführt werden kann.