Calculation of settlements with the subgrade reaction method

The subgrade reaction method represents a linear-elastic stress-deformation behavior of the soil. The flexurally rigid foundation lying on the ground is bedded with springs representing the yielding soil. The method is based on Winkler's hypothesis, which assumes a linear relationship between the subsoil and the base stresses.

The subsoil is replaced by individual springs that are decoupled from each other:

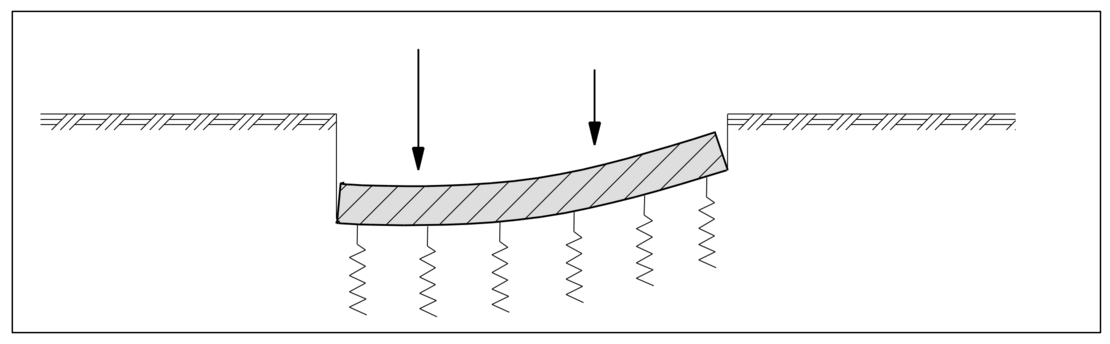
Each spring is loaded or compressed by the stresses acting on them. No shear strength of the soil is assumed, so that the influence of neighboring pressure on the underlying soil layers is not taken into consideration. Thus, the contribution to carry loads of the surrounding soil is not covered by this method.

The subgrade reaction method can be used for systems in which the extensive involvement of the surrounding soil is not to be expected, or which have a large dimension in one direction so that activation of the shear stiffness is not important, e.g. for long roads, runways or similar. If settlements of individual foundations located close to each other are to be calculated, the method is less suitable, since the shear stiffness and the mutual influence of the individual foundations are not taken into considerations.

The modulus of subgrade reaction k_s describes the relationship between the pressure on the underlying soil layers and the resulting settlement s of the soil:

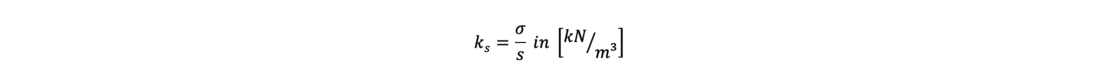
If the values of the modulus of subgrade reaction are the same over the considered foundation area, a uniform load does not result in a settlement depression, but in a uniform settlement of a foundation, provided that the slab has the same thickness at each location. This results in a discontinuity of settlements at the edges of the foundation, see figure above. The discontinuity illustrates that the shear stiffness of the soil is not taken into consideration.

It is important to understand that the modulus of subgrade reaction does not represent a constant value but depends on the stiffness of the structure and its distribution over the foundation base. Even for the same soil properties in the area of a foundation base, different moduli of subgrade reaction must generally be applied. The modulus of subgrade reaction is not constant for a foundation base!

The following differential equation describes the problem of a bedded slab and is mostly solved numerically:

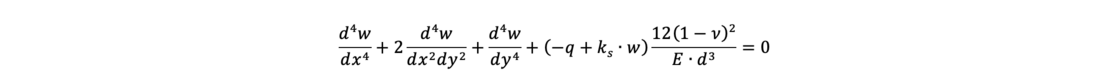
with

w:        settlement of slab [m]

d:         thickness of slab [m]

E:        Young’s modulus of slab [kN/m²]

n:         Poisson’s ratio of the concrete [-]

ks:        modulus of subgrade reaction [kN/m³]

q:         area load [kN/m²]

The computer program GGU-SLAB takes into consideration the stiffness of the foundation slab and other building components (e.g. walls, beams, etc.) for determining state variables and the settlement of the foundation slab, also using the subgrade reaction method. Beams can be defined along nodes of the FE mesh, which are taken into consideration in the computations with regard to their stiffness. This is useful, for example, if the influence of foundation beams, walls, top beams, etc. is to be taken into consideration. A foundation beam can also be modeled by thickening the slab in the corresponding area.

System stiffnesses can also be considered using the computer program GGU-SETTLE, which does not allow for slab stiffness.

This requires an iterative solution strategy with a close cooperation between the geotechnical engineer and the structural engineer:

In a first iteration step, the calculation is performed (by the structural engineer) for a bedded system that takes the elastic system stiffnesses of the whole structure into account. For this purpose, a reasonable distribution of the subgrade reaction modulus over the foundation area is assumed. This results in a base pressure distribution on the underlying soil that varies over the foundation area due to varying system stiffnesses. This distribution of the base pressure is used as the area load in another calculation of settlements (by the geotechnical engineer). This, in turn, results in a modified distribution of subgrade moduli below the foundation base, which is taken into account in the next iteration step in the structural engineer's system and again results in a modified base pressure on the underlying soil.

If the calculated values for the base pressures on the underlying soil of two successive iteration steps no longer differ significantly, the iteration can be terminated.

For general information on the use of this program, please refer to the glossary entry "Calculation of settlement in geotechnics".

For the example shown below of a 30 cm thick foundation slab with a non-uniform loading between σ₀  = 60 kN/m² and σ₀  = 240 kN/m², the following video shows how a settlement analysis with the design of the reinforced concrete slab using the subgrade reaction method can be performed using the GGU-SLAB program.