Setzungsberechnung einer Bodenplatte mit dem Steifemodulverfahren
Inhaltsverzeichnis
1. Steifemodulverfahren
Um die Interaktion zwischen Baugrund und Gebäude korrekt abzubilden, kann das Steifemodulverfahren verwendet werden. Mit den Berechnungen nach dem Steifemodulverfahren werden iterativ die Sohlspannungen ermittelt, bei denen die Biegelinie des biegesteifen Fundaments mit der Setzungsmulde des anstehenden Bodens gleich sind.
Die Setzung an einem betrachteten Ort hängt nicht nur von dem direkt dort wirkenden Sohldruck ab, sondern auch von den Sohlspannungen an benachbarten Orten und somit von der gesamten flächigen Belastung.
Die Setzungsmulde entspricht somit auch der Biegelinie des Fundaments, vgl. nachfolgendes Bild.
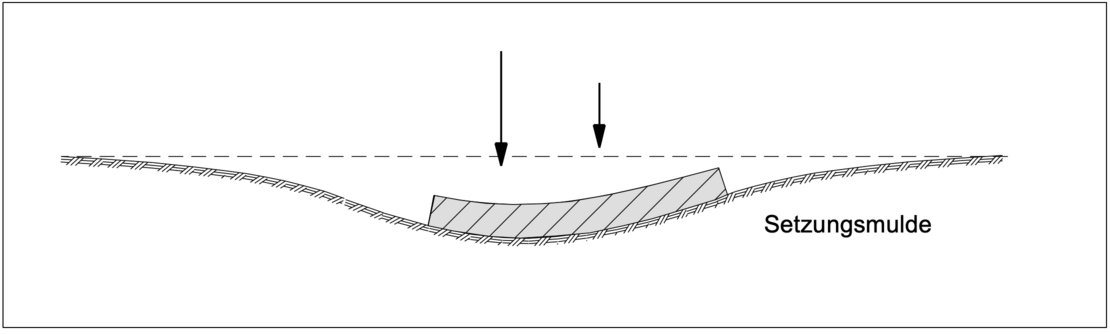
Es wird also – anders als beim Bettungsmodulverfahren - eine Schubfestigkeit des Bodens angenommen, so dass die Setzungsmulde auch über die belastete Sohlfläche hinaus geht und die wirkenden Sohlpressungen in dem den Berechnungen zugrunde liegenden weiteren elastischen Halbraum Setzungen verursacht.
Ein Lösungsverfahren wird von Ohde vorgeschlagen. Dort wird die o.g. Bedingung in den Elementmittelpunkten erfüllt, dass sich die Biegelinie des biegesteifen Fundaments und die Setzungsmulde des Bodens gleichen müssen.
Auch numerische Methoden wie die FEM stehen zur Lösung des Problems zur Verfügung, so auch das Programm GGU-SLAB. Dort wird – ähnlich wie beim Bettungsmodulverfahren mit iterativer Verbesserung der Bettungsmoduli nach Ahrens und Winselmann – im ersten Schritt die Biegelinie einer gebetteten Platte nach der Dgl.
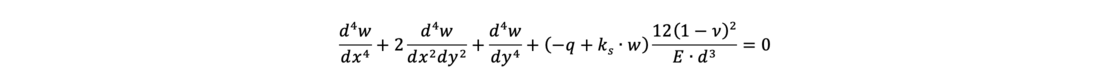
berechnet. Dabei sind
- w: Durchbiegung der Platte [m]
- d: Dicke der Platte [m]
- E: Elastizitätsmodul der Platte [kN/m²]
- ν: Querkontraktionszahl des Betons [-]
- ks: Bettungsmodul [kN/m³]
- q: Flächenlast [kN/m²]
Die daraus resultierende Sohldruckverteilung wird als Belastung in einer Setzungsberechnung am elastischen Halbraum angesetzt. Stimmen Setzungsmulde und Biegelinie der Platte nicht überein, werden die Bettungsmoduli in weiteren Iterationsschritten so lange varriert, bis sich die Setzungsmulde und die Biegelinie bis auf eine vom Anwender vorgegebene Genauigkeitsgrenze gleichen.
Wie bei allen Finite-Elemente-Analysen liegt diese Näherungslösung mit einer feineren werdenden Elementierung immer näher an der exakten Lösung.
2. Berechnungsbeispiel
Für das unten gezeigte Beispiel einer 30 cm dicken Fundamentplatte mit gleichmäßiger Belastung von σ0 = 120 kN/m² wird im nachfolgenden Video gezeigt, wie mit dem Programm GGU-SLAB eine Setzungsberechnung mit Bemessung der Stahlbetonplatte nach dem Steifemodulverfahren durchgeführt werden kann.
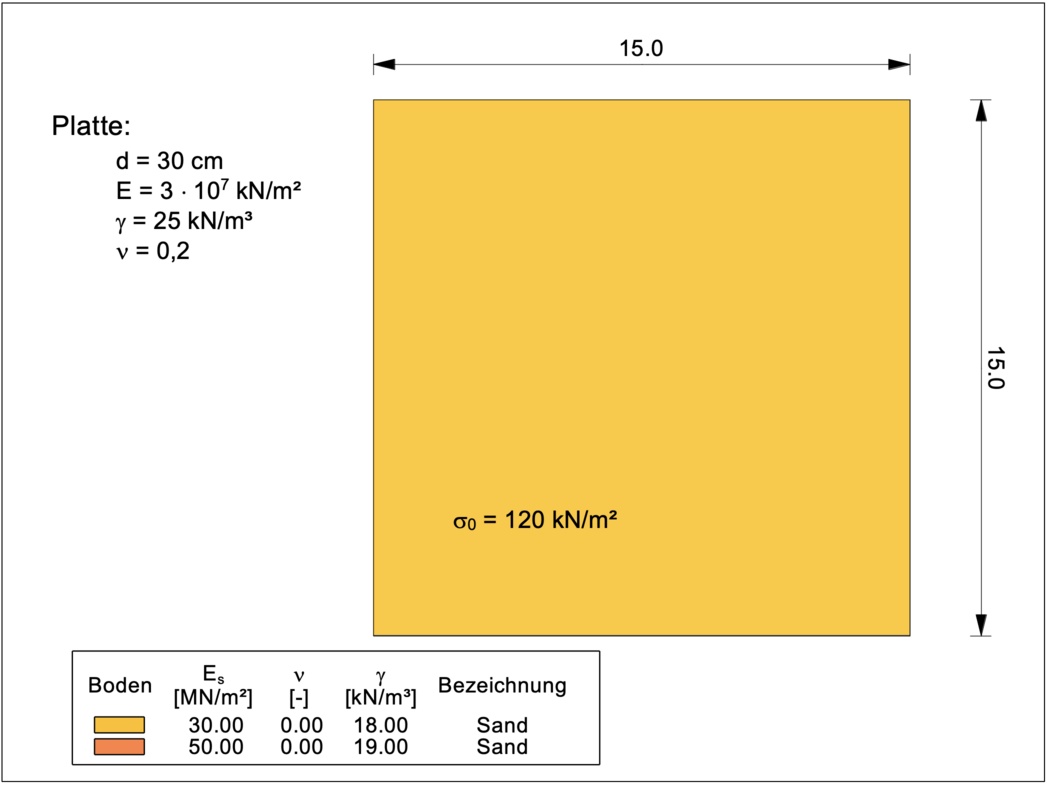
Hinweise zur Nutzung
Alle hier aufgeführten Texte, Bilder und Medien unterliegen dem Urheberrecht und sind geistiges Eigentum der Civilserve GmbH. Verwendung ist nur mit entsprechendem Hinweis und einer Verlinkung auf diese Quelle erlaubt.