Calculation of settlements with the constrained modulus method

The constrained modulus method can be used to correctly represent the interaction between the subsoil and the building. With the calculations according to the constrained modulus meth-od, the base stresses are determined iteratively for which the bending of the flexurally stiff foundation equals the settlement depression of the foundation base. 

The settlement at a given location depends not only on the pressure on the underlying soil acting directly there, but also on the stresses at neighboring locations and thus on the total load area.

The settlement depression thus also corresponds to the bending of the foundation, cf. the following figure.

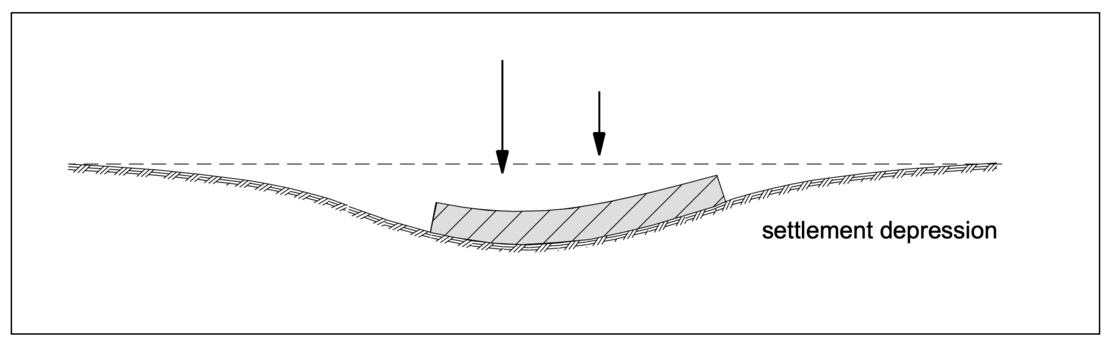
Thus, in contrast to the subgrade reaction method, the shear strength of the soil is taken into consideration, so that the settlement depression also extends beyond the loaded base area and the acting pressures on the underlying soil cause settlements in the elastic half-space on which the calculations are based.

A solution procedure is proposed by Ohde. There, the above-mentioned condition is fulfilled in the element centers that the bending of the flexurally rigid foundation and the settlement depression of the soil must be the same. 

Numerical methods such as the Finite Element Method are also available for solving the problem, as in the computer program GGU-SLAB. There - similar to the subgrade reaction method with iterative improvement of the subgrade reaction moduli according to Ahrens and Winselmann - in the first step the bending of a bedded slab is calculated according to the differential equation

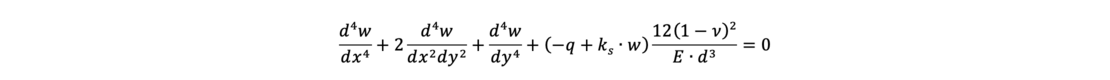
with

w:        settlement of slab [m]

d:         thickness of slab [m]

E:        Young’s modulus of slab [kN/m²]

n:         Poisson’s ratio of the concrete [-]

ks:        modulus of subgrade reaction [kN/m³]

q:         area load [kN/m²]

The resulting distribution of the pressure on the underlying soil is applied as a load in a settlement calculation on the elastic half-space. If the settlement depression and the bending of the slab do not match, the subgrade reaction moduli are varied in further iteration steps until the settlement depression and the bending resemble each other to within an accuracy limit specified by the user.

As with all finite element analyses, this approximate solution is closer to the exact solution with finer elements.

For the example shown below of a 30 cm thick foundation slab with a uniform loading of σ₀ = 120 kN/m², the following video shows how the computer program GGU-SLAB can be used to perform a settlement analysis with a design of the reinforced concrete slab using the constrained modulus method.