Böschungsbruch
Inhaltsverzeichnis
1. Böschungsbruch & Geländebruch
Das Abrutschen eines Gleitkörpers entlang einer Gleitlinie, in der der Scherwiderstand des Bodens überschritten wird, wird als Böschungsbruch bezeichnet. Das Abrutschen eines Stützbauwerks (z.B. Verbauwände, Winkelstützmauern, etc.) mit einem Teil des umgebenden Erdreichs entlang einer Gleitlinie, in der der Scherwiderstand des Bodens überschritten wird, wird als Geländebruch bezeichnet.
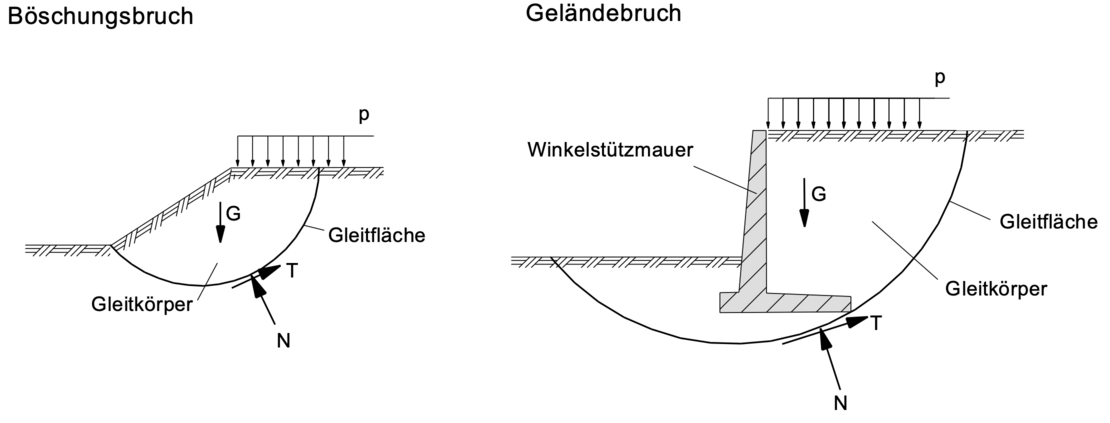
Die zu untersuchenden Bruchmechanismen und die anzuwendenden Berechnungsverfahren werden in der Geländebruchnorm DIN 4084 beschrieben, auf die DIN 1054 im Abschnitt „Gesamtstandsicherheit“ Bezug nimmt. Diese Nachweise werden nach DIN 1054 für den Grenzzustand GEO-3 (Nachweisverfahren 3) geführt.
Für praktische Nachweise werden für die Gleitkörper einfache geometrische Formen gewählt. Bevorzugt wird von einem Kreis ausgegangen. Dabei wird die Lage des Mittelpunkts des Gleitkreises variiert, um Radius und Lage des ungünstigsten Kreises zu bestimmen. Im Bruchszustand wird der Gleitkörper als starr angenommen, nur entlang der Gleitfläche treten Relativbewegungen auf.
Im Regelfall verläuft die ungünstigste Gleitfläche bei einem Böschungsbruch bei homogenem Boden mit einem inneren Reibungswinkel von φ’ > 5° durch den Fußpunkt der Böschung, bei einem Geländebruch durch den erdseitigen Fußpunkt der Gründung des Stützbauwerks, vgl. vorstehende Bilder.
2. Berechnungsverfahren
Zur Berechnung der Standsicherheit stehen nach DIN 4084 grundsätzlich die folgenden Verfahren zur Verfügung:
- Lamellenverfahren: kreisförmige und nicht kreisförmige Gleitlinien
- Lamellenfreie Verfahren bei kreisförmigen Gleitlinien
- Verfahren mit geraden Gleitlinien
- Verfahren mit Blockgleitlinien
- Verfahren mit inneren Gleitlinien
In den meisten Fällen reicht es aus, Kreise als mögliche Gleitlinien zu wählen. Bei Geländesprüngen mit Stützbauwerken, bei Klüften oder geradlinigen Störzonen bzw. Schichten mit geringer Scherfestigkeit und bei Böschungen, bei denen konstruktive Elemente mitwirken, sind gerade Gleitlinien und zusammengesetzte Bruchmechanismen geeignet, vgl. unten dargestellte, mit GGU-STABILITY berechnete Beispiele.
Lamellenverfahren mit kreisförmiger Gleitlinie:
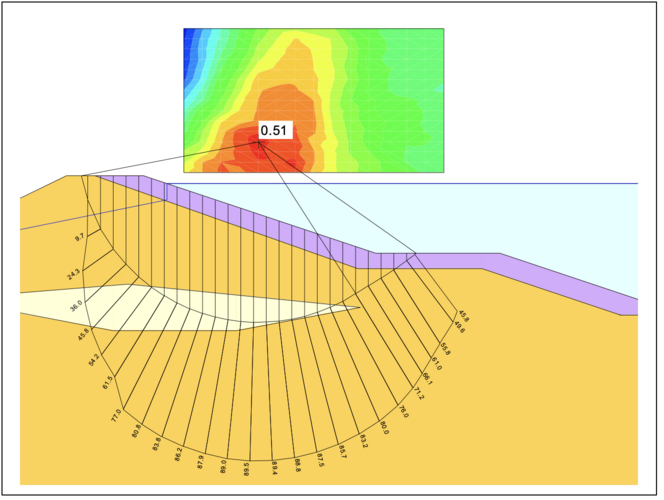
Verfahren mit inneren Gleitlinien:
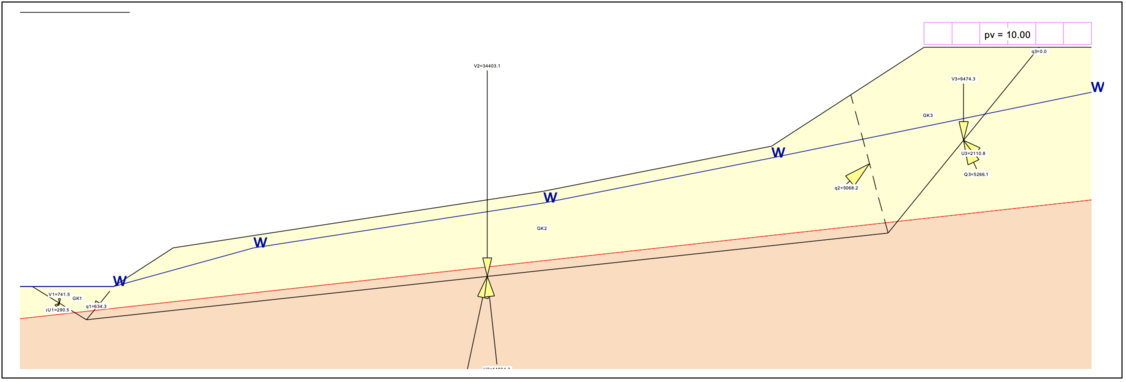
Lamellenverfahren mit kreisförmiger Gleitlinie durch erdseitigen Fußpunkt der Gründung:
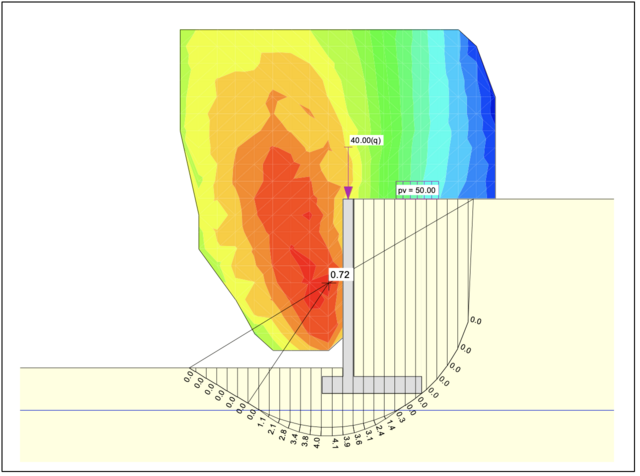
Verfahren mit Blockgleitlinien, hier unter Berücksichtigung von Zuggliedern:
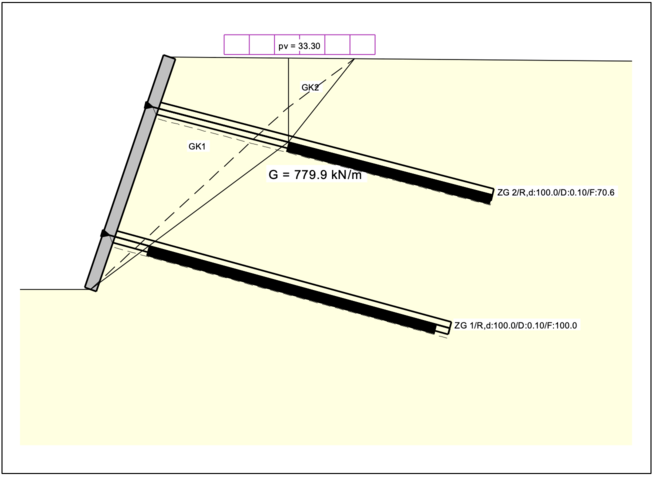
Bei allen Systemen muss die Lage der ungünstigsten Gleitlinie bestimmt werden und ist nicht bekannt. Die Berechnung der Standsicherheit an mehreren Gleitlinien liefert dann die geringste Sicherheit.
Im Hinblick auf die zur Ermittlung der Böschungs- bzw. Geländebruchsicherheit in Frage kommenden Bruchmechanismen und Berechnungsverfahren verweist DIN 1054 auf die DIN 4084.
3. Berücksichtigung von Grundwasser
Ansatz des Strömungsdrucks durch hydrostatische Wasserdruckdifferenz
Anstehender Wasserdruck kann vereinfachend als eine in horizontaler Richtung wirkende Kraft bis zur Unterkante der (hier: kreisförmigen) Gleitfläche angenommen werden. Wenn das Außenwasser niedriger steht als das Grundwasser strömt das Wasser seinem Gefälle nach ab und belastet das Korngerüst des Böschungsbodens mit einem Strömungsdruck. Eine einfache, aber auf der sicheren Seite liegende Abschätzung besteht darin, den hydrostatischen Wasserüberdruck als äußere Horizontalkraft W anzusetzen.
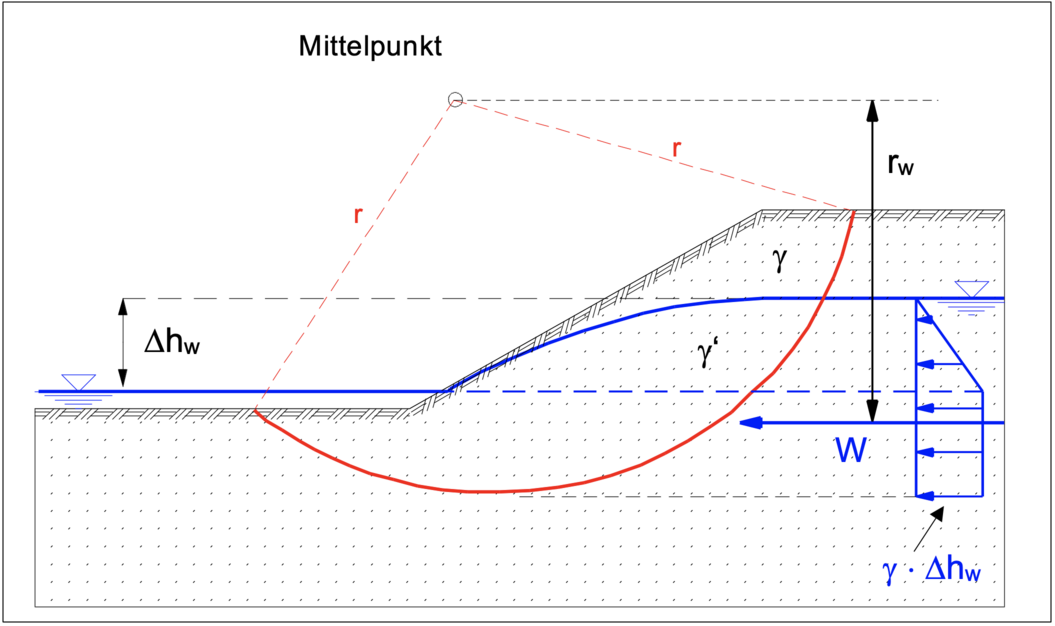
Ansatz des Wasserdrucks aus Potentialströmung
Entgegen zum vorhergehenden Nachweisverfahren werden bei diesem Verfahren Porenwasserdrücke mit in die Berechnung aufgenommen. Entlang der angenommenen (hier: kreisförmigen) Gleitfläche müssen daher auch die Porenwasserdrücke bekannt sein. Dies bedeutet, dass vor der Berechnung der Standsicherheit der Böschung eine untergrundhydraulische Berechnung zur Ermittlung des Potentialliniennetzes geschaltet werden muss.
Für den durchströmten Bereich des Bruchkörpers wird die Gesamtlast aus Bodenlast und Wasserlast angesetzt, falls vorhanden auch Verkehrs- und Baulasten.
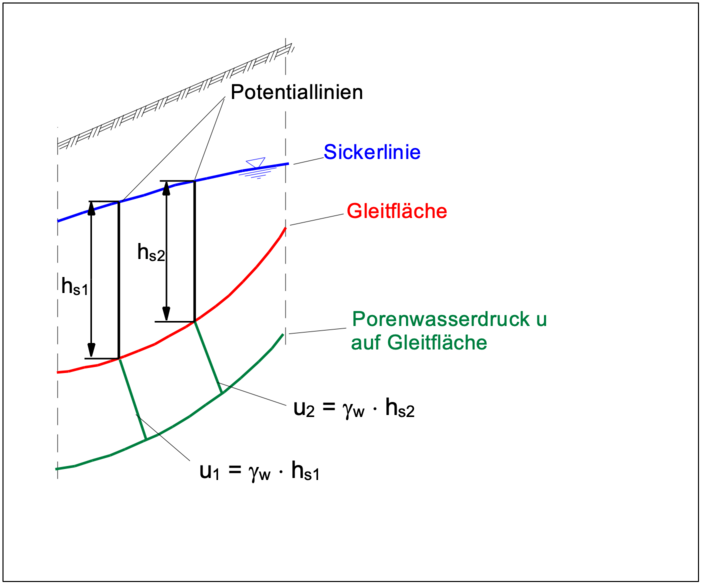
Falls kein Potentialliniennetz zur Verfügung steht, kann der Porenwasserdruck u näherungsweise in einem Punkt der Gleitfläche ausreichend genau ermittelt werden, in dem zur Berechnung mit

für hS der Abstand lotrecht über dem betrachteten Punkt bis zur Sickerlinie angesetzt wird.
4. Maßgebende Gleichungen für kreisförmige Gleitlinien
Zur Bestimmung der Standsicherheit einer Böschung werden rückhaltende Momente zu den antreibenden Momenten in Relation gesetzt. Antreibende Momente werden aus Eigengewicht, Wasserüberdruck und Verkehrslasten gebildet. Rückhaltende Momente resultieren aus den Reibungskräften entlang der kreisförmigen Gleitlinie. Die rückhaltenden Scherkräfte in der Gleitfuge sind abhängig von der Normalkraft auf das Gleitlinienelement.
4.1 Ansatz des Strömungsdrucks durch hydrostatische Wasserdruckdifferenz
Die iterativ zu lösende Gleichung zur Bestimmung des Ausnutzungsgrads μ lautet für die Berechnung und der Unterteilung des Gleitkörpers in „i“ Lamellen:
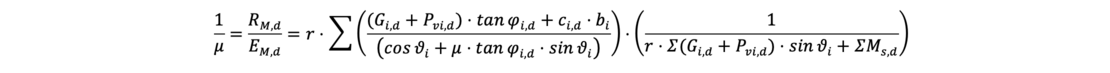
Das zusätzliche Moment ∑Ms,d aus der charakteristischen Wasserdruckresultierenden Wk mit dem Hebelarm rw wird bei den Einwirkungen mit erfasst:
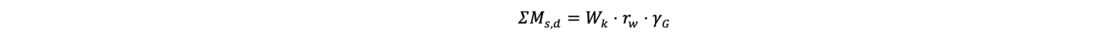
Für den Fall einer wassergesättigten Lamelle ist das Gewicht G‘i der unter Auftrieb stehenden Lamelle zu verwenden.
Der Bemessungswert der Scherparameter wird wie folgt berechnet:
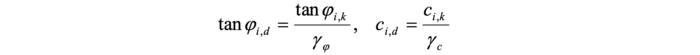
Pvi,d stellt den Bemessungswert einer äußeren vertikalen Einwirkung P auf der Lamelle i mit der Breite bi dar. ϑ beschreibt den Winkel zwischen der Verbindung des gewählten Mittelpunkts des Gleitkreises und der Mitte der Lammellenunterseite und der Senkrechten dar.
4.2 Ansatz des Wasserdrucks aus Potentialströmung
Die genauesten Ergebnisse erreicht man unter vorheriger Berechnung des Potentialliniennetzes und Ansatz der Potentialdrücke entlang der Bruchlinie. Gerade bei stark gekrümmten Stromlinien und steilen Wasserspiegellinien wird die Erhöhung der effektiven Spannungen berücksichtigt, so dass die Sicherheit „genauer“ berechnet wird. Die iterativ zu lösende Gleichung zur Bestimmung des Ausnutzungsgrads μ lautet für die Berechnung und der Unterteilung des Gleitkörpers in „i“ Lamellen:
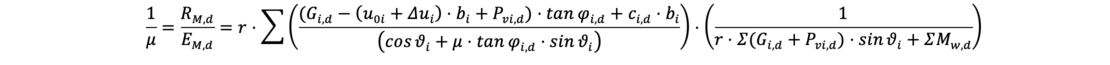
Der Term ΣMw,d resultiert hierbei aus auf der Böschung wirkenden horizontalen und vertikalen Wasserdrücken.
Der Porenwasserdruck setzt sich zusammen aus zwei Anteilen, dem Porenwasserdruck u0i in der Lamelle i und dem Porenwasserüberdruck Δui infolge einer eventuellen Konsolidation des Bodens der Lamelle i.
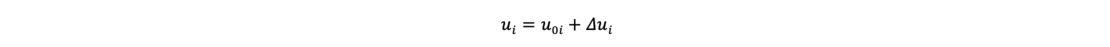
Für den Fall einer wassergesättigten Lamelle wird das (totale) Gewicht Gi berechnet zu:
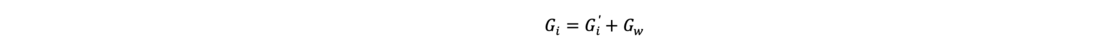
5. Standsicherheitsbeeinflussende Größen
Böden:
- Die Standsicherheit von Böschungen hängt ab von der Schichtung der Böden. Geologische Störzonen, und nicht gewachsene, sondern aufgefüllte Böden reduzieren die Standsicherheit.
Das Vorhandensein von Wasser hat maßgeblichen Einfluss auf die Standsicherheit:
- Porenwasserüberdruck: Vorhandener Porenwasserüberdruck reduziert die Korn-zu-Korn-Spannungen (Normalspannung) und verringert damit die mögliche aufnehmbare Scherkraft in der Scherfuge. Die Sicherheit wird reduziert.
- Grundwasser: Vorhandenes Grundwasser im Damm erzeugt im Hang einen Strömungsdruck zum Böschungsfuß hin. Bei Austritt des Wassers am Hang können Auswaschungen auftreten, was die Standsicherheit verringert.
- Tagwasser: Niederschlag und weitere Zuflüsse von Wasser können zu Auswaschungen führen, was die Standsicherheit verringert.
- Wasser in Seen und Flüssen: Wellenschlag kann den Hang erodieren, was die Standsicherheit verringert. Bei schnellem Wasserpegelabfall müssen die daraus resultierenden Porenwasserüberdrücke beachtet werden.
Veränderliche Einwirkungen (Verkehrslasten):
- Veränderliche Einwirkungen im unmittelbaren Böschungsbereich reduzieren die Standsicherheit.
6. Berechnungen zum Geländebruch
Der Geländebruch hat die gleichen bodenmechanischen Bruchmechanismen wie der Böschungsbruch. Daher unterscheiden sich die Berechnungsverfahren nicht von denen, die für den Böschungsbruch hergeleitet wurden.
Innerhalb des abrutschenden Gleitkörpers befindet sich eine Stützkonstruktion, deren Eigengewicht bei der Berechnung zu berücksichtigen ist, die jedoch auf die zugrunde liegende Bruchmechanik keinen Einfluss hat.
Mit den Programmen
- GGU-CANTILEVER (Winkelstützwände)
- GGU-UNDERPIN (Unterfangungen)
- GGU-GABION (Stützkonstruktionen aus Beton-Elementen, Blockschichtungen und Gabionen)
- GGU-RETAIN (Bemessung von Spundwänden, Trägerbohlwänden, Ortbetonwänden, FMI-Wänden und kombinierten Spundwänden)
können weitere, für Stützkonstruktionen und Verbauten notwendige Standsicherheitsuntersuchungen durchgeführt werden. Diese Programme bieten eine sehr komfortable Schnittstelle zum Programm GGU-STABILITY zur schnellen Untersuchung der Geländebruchsicherheit.
7. Berechnungsbeispiel, Video: Nachweis der Böschungsbruchsicherheit
Für das unten gezeigte Beispiel einer Böschung, die auf der Böschungsoberkante mit einer veränderlichen Einwirkung von p = 20 kN/m² belastet ist, wird im nachfolgenden Video gezeigt, wie mit dem Programm GGU-STABILITY der Nachweis der Böschungsbruchsicherheit geführt werden kann.
Zur Generierung des Systems wird das äußerst praktische und anwenderfreundliche Menu „Gängige Systeme“ verwendet.
Hinweise zur Nutzung
Alle hier aufgeführten Texte, Bilder und Medien unterliegen dem Urheberrecht und sind geistiges Eigentum der Civilserve GmbH. Verwendung ist nur mit entsprechendem Hinweis und einer Verlinkung auf diese Quelle erlaubt.