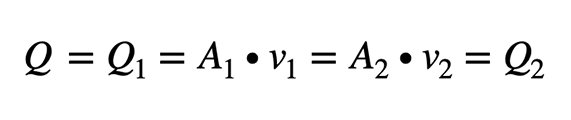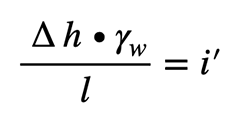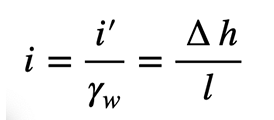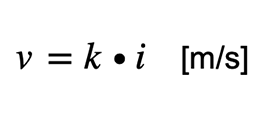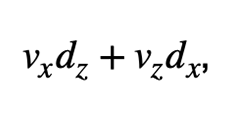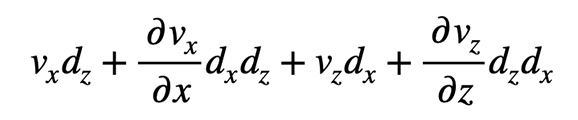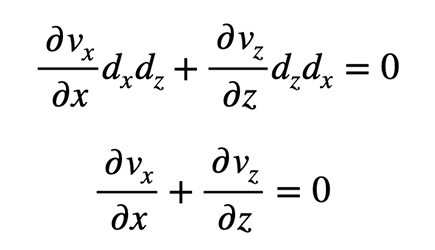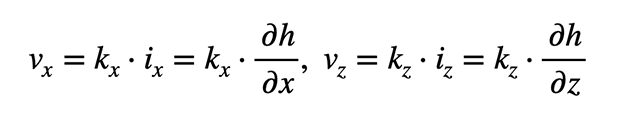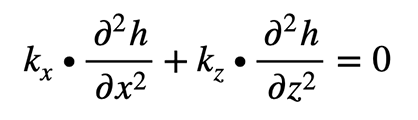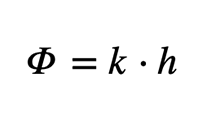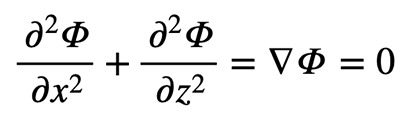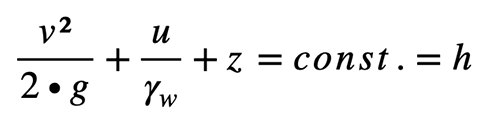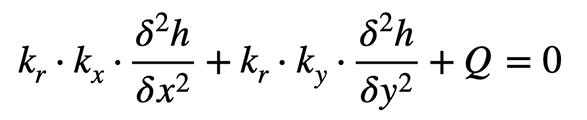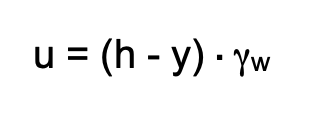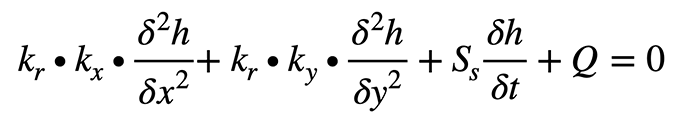Berechnung von instationären Grundwasserströmungen
Inhaltsverzeichnis
1. Grundwasserströmungen verstehen
Eine Einführung in die Bewegung des Untergrundwassers
Zur Beschreibung der Bewegung des Grundwassers wird eine Filterströmung betrachtet. Zwei Gleichungen aus der Hydromechanik liegen der mathematischen Beschreibung dieser Grundwasserströmung zugrunde:
- Kontinuitätsgleichung
- Darcy’sches Gesetz
1.1 Kontinuitätsgleichung
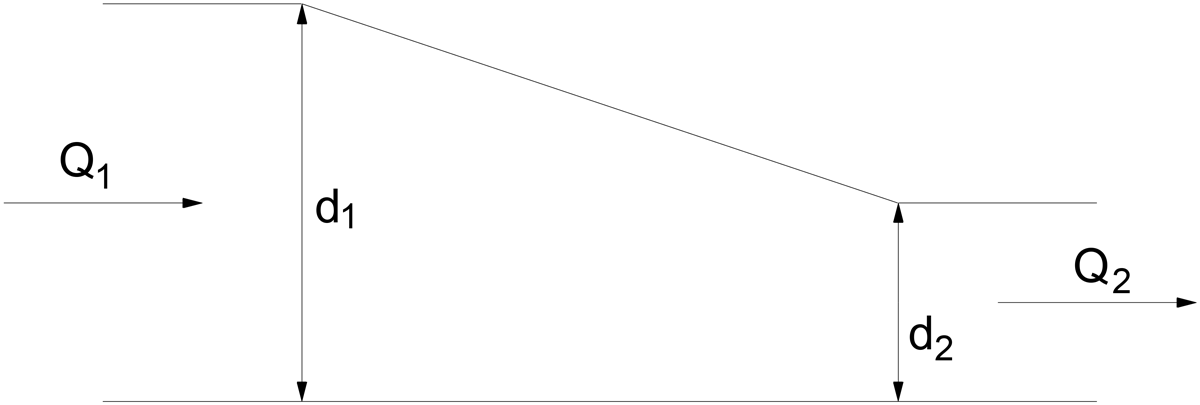
Die Kontinuitätsgleichung beschreibt, dass sich die Masse einer inkompressiblen Flüssigkeit (mit konstanter Dichte) in einem „Kontrollraum“ nicht ändern kann. Das Produkt aus Geschwindigkeit und durchströmter Querschnittsfläche ist gleich:
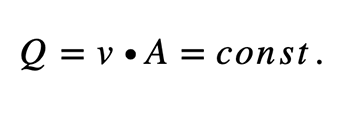
1.2 Darcy’sches Gesetz – Die Basis der Grundwasserströmungen
mit
v: Filtergeschwindigkeit [m/s]
k: Durchlässigkeitsbeiwert [m/s]
i: hydraulisches Gefälle [-]
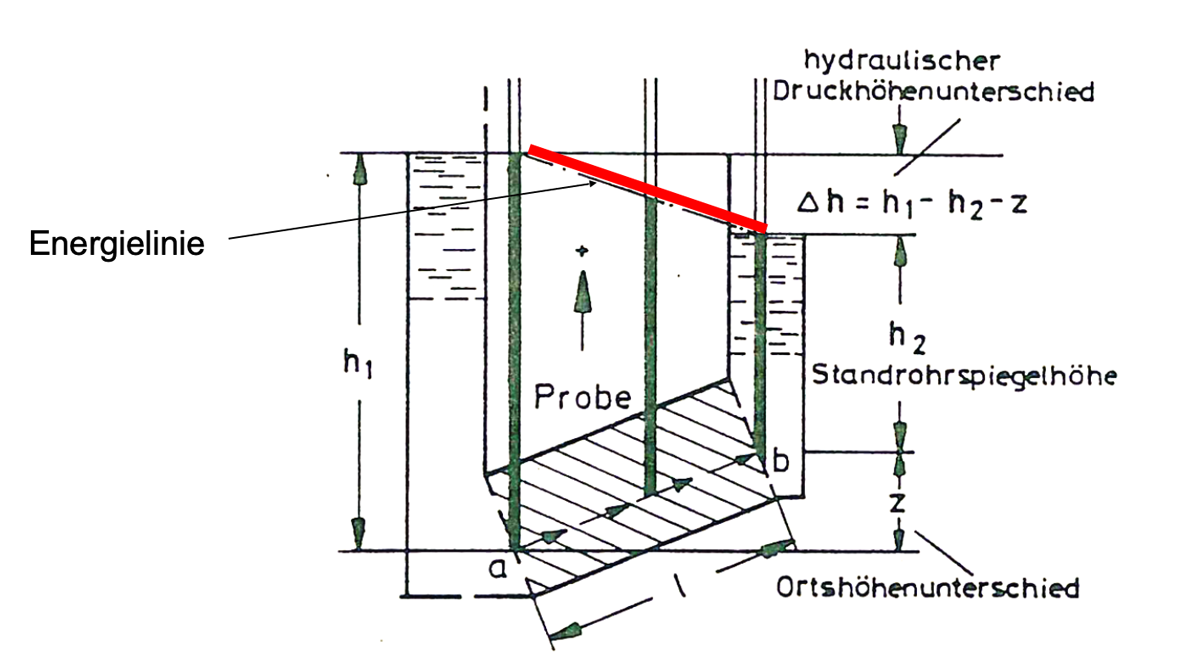
Bei der Durchströmung des Bodens wird der Potentialunterschied abgebaut, d.h. es wird Energie umgewandelt. Dies lässt sich mit Hilfe einer Energielinie darstellen.
Die Geschwindigkeit des Wassers wird nun definiert als Durchflussmenge in der Zeiteinheit, bezogen auf die Einheit der auf den Strömungslinien senkrechten gesamten Querschnittsflächen. Dieser Wert, die sogenannte Filtergeschwindigkeit, ist nicht die tatsächliche Geschwindigkeit der Wasserteilchen, da die Durchflussfläche aufgrund des Vorhandenseins von Bodenteilchen nur einen Teil der gesamten Querschnittsfläche ausmacht. Weitere Geschwindigkeitsdefinitionen finden sich in der folgenden Abbildung:
2. Laplace’sche Strömungsgleichung
Grundwasserströmungen treten natürlich bzw. aufgrund von baulichen Maßnahmen infolge unterschiedlicher Grundwasserspiegelhöhen auf. Im Folgenden wird eine ebene, stationäre Grundwasserströmung mathematisch beschrieben, um baupraktische Probleme damit beschreiben zu können. Dabei gelten die grundlegenden Annahmen:
- Gültigkeit des Darcy’schen Gesetzes
- Wasser und Boden sind inkompressibel
- Homogenität und Isotropie
- Keine Kapillarkräfte, nur freies Grundwasser
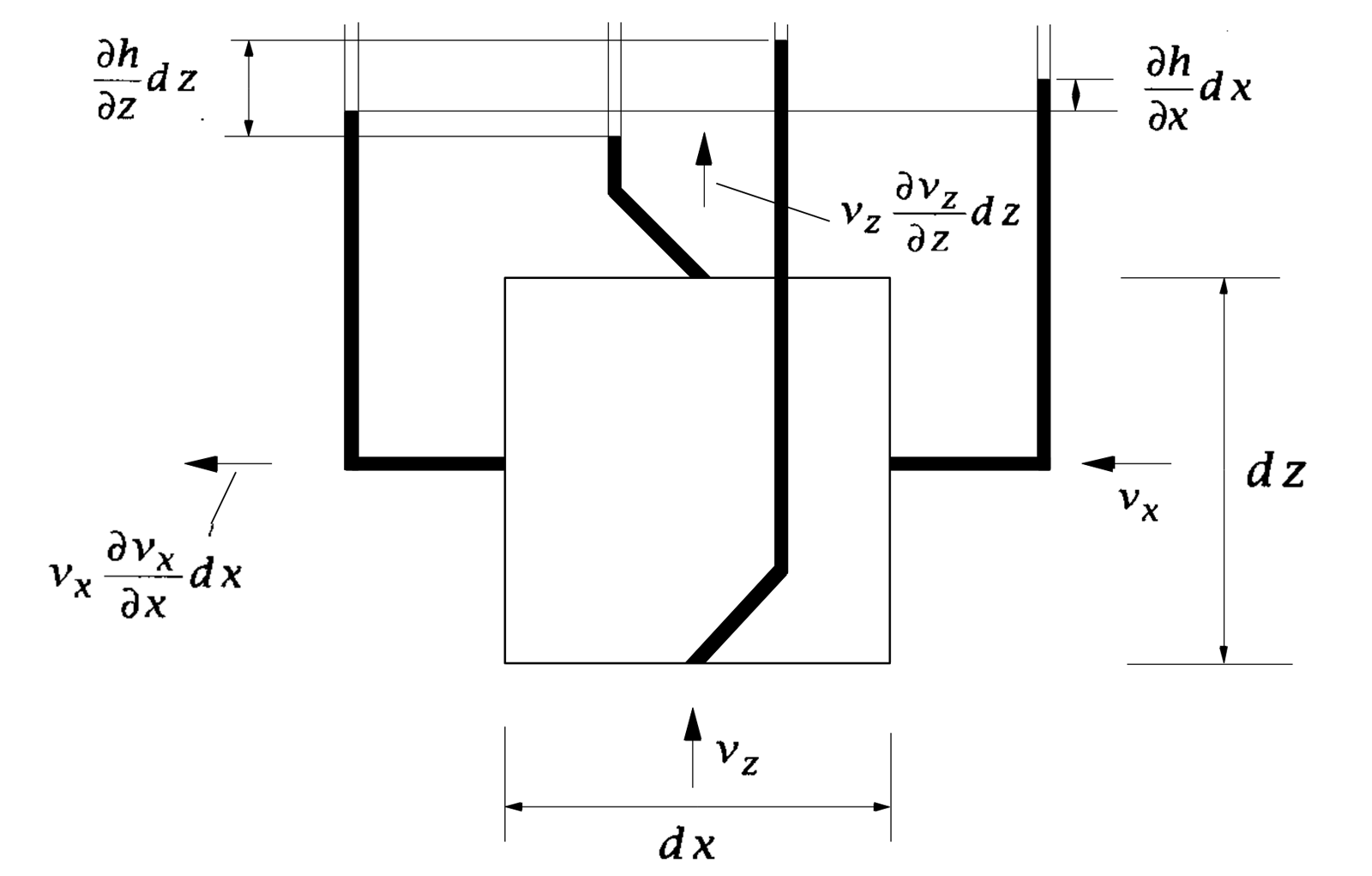
Aus dem durchströmten Boden wird gedanklich ein prismatisches Bodenelement mit den Kantenlängen dx, dy und dz geschnitten, das den genannten Annahmen genügt. Die Kantenlänge senkrecht zur Bildebene ist zu dy =1 gewählt.
Die waagerechte Komponente der Strömungsgeschwindigkeit ist vₓ, der hydraulische Gradient in waagerechter Richtung iₓ. h ist die hydraulische Druckhöhe am Element. Die entsprechenden Werte in der vertikalen Richtung z sind vz und iz. Die Strömung ist zweidimensional. In der Richtung y ist der Gradient und daher auch die Wassergeschwindigkeit Null.
Eingesetzt in die Kontinuitätsgleichung führt dies zur Laplace’schen Strömungsgleichung, die besagt, dass bei gleichbleibendem Rauminhalt eine Veränderung des Gradienten in Richtung z durch eine Veränderung mit entgegengesetztem Vorzeichen in der Richtung x ausgeglichen werden muss. Für isotrope Durchlässigkeitsverhältnisse mit kx = kz gilt somit:
Sie beschreibt die Sickerströmung in porösen Medien. Die Lösung dieser Differentialgleichung bedarf der Formulierung von Randbedingungen, die in Folgenden beschrieben werden.
3. Randbedingungen für Grundwasserströmungen
Zur Lösung der o.g. Differentialgleichung müssen Randbedingungen formuliert werden. Man unterscheidet dabei in:
- Randbedingungen 1. Art, Potentialrandbedingungen, Rand offen: Definition von einem Grundwasserpotential „h“ am Modellrand.
- Randbedingungen 2. Art, Quellenrandbedingungen, Rand offen: Definition von Quellen „q“ am Modellrand.
- Natürliche Randbedingung, Rand "dicht", undurchlässiger Rand: Zu- oder Abfluss gleich Null.
4. Das Potential bei der Grundwasserströmung
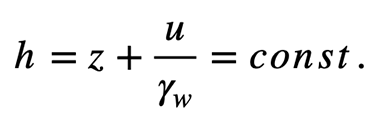
mit
g: Erdbeschleunigung [m/s²]
z: geodätische Höhe [m], bezogen auf eine gewählte Bezugsebene
u: Wasserdruck [kN/m²]
γw: Wichte des Wassers [kN/m³]
und ergibt sich aus den Anteilen der Lage- Druck- und Geschwindigkeitsenergie. Die Geschwindigkeitshöhe v²/2⋅g kann wegen der im Untergrund vorkommenden kleinen Fließgeschwindigkeiten im allgemeinen vernachlässigt werden. Somit bilden die geodätische Höhe und die Druckhöhe das Potential der Bewegung:
5. Stationäre Berechnungen von Grundwasserströmungen mit GGU-2D-SSFLOW
Darin bedeuten:
kx, ky: Durchlässigkeit für x- und y-Richtung, z.B. [m/s]
h: Standrohrspiegelhöhe, in [m]
kr: Beiwert zur Bestimmung der Durchlässigkeit im ungesättigten Bereich [-]
Q: Wassermenge, z.B. in [m³/s]
x,y: Koordinaten, z.B. in [m]
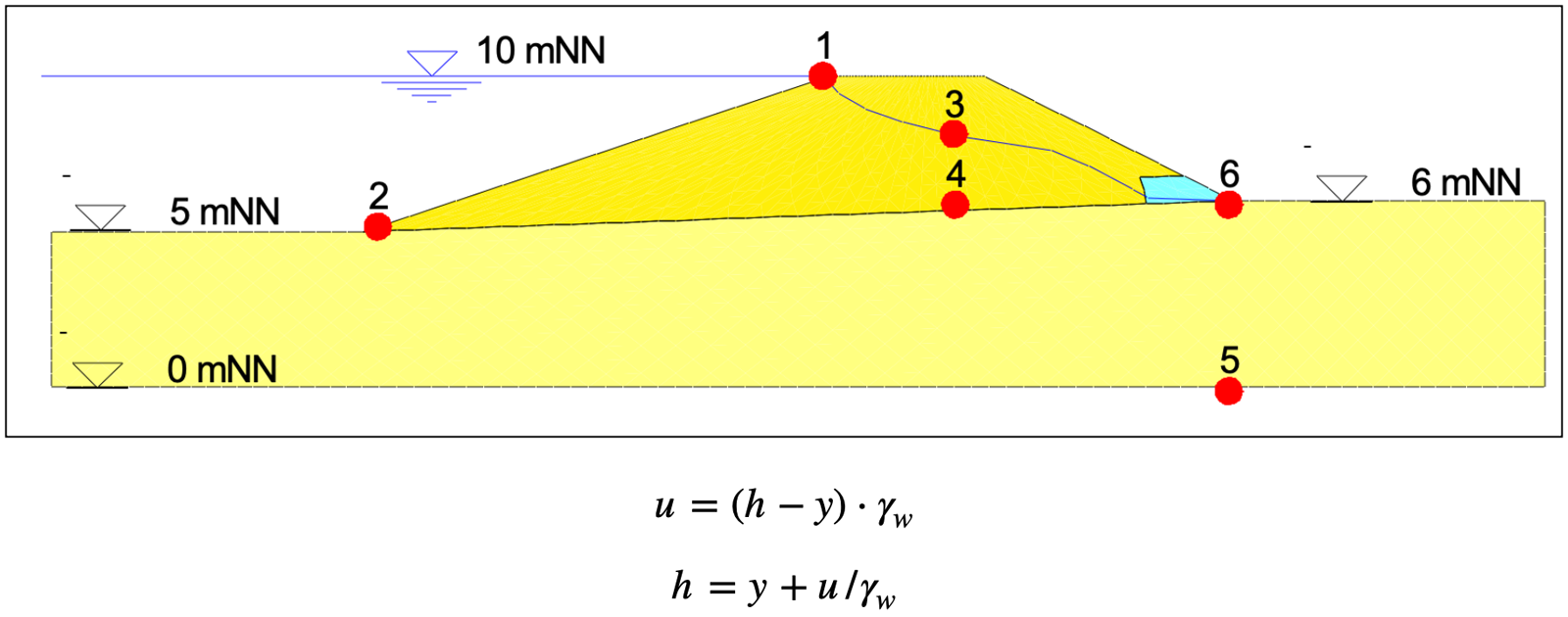
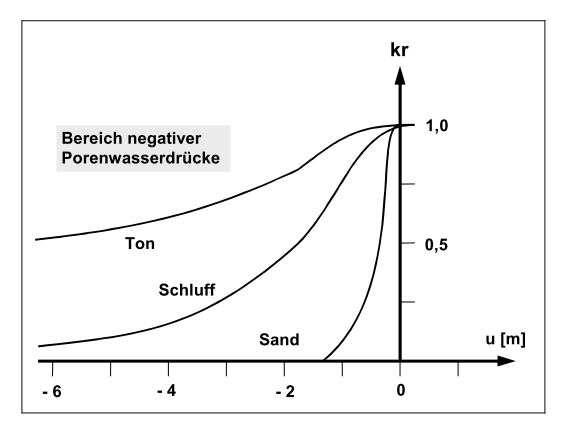
Der Wert kr erfasst die Veränderung der Durchlässigkeit in der ungesättigten Zone r oberhalb des Grundwasserspiegels und kann zwischen 0.0 und 1.0 liegen. In gesättigten Systembereichen ist kr gleich 1.0. Der Wert kr ist eine Funktion des Porenwasserdrucks u. Der Porenwasserdruck u berechnet sich aus der Standrohrspiegelhöhe h, der Ortshöhe y und der Wichte des Wassers γw .
6. Instationäre Berechnungen mit GGU-2D-TRANSIENT
GGU-2D-TRANSIENT ermöglicht die Berechnung von instationären Grundwasserströmungen in horizontal ebenen, vertikal ebenen und rotationssymmetrischen Grundwassersystemen nach der Finiten-Element-Methode. Die zu lösende Differentialgleichung lautet für vertikal ebene Systeme:
Darin bedeuten:
kx, ky: Durchlässigkeit für x- und y-Richtung, z.B. [m/s]
h: Standrohrspiegelhöhe, in [m]
kr: Beiwert zur Bestimmung der Durchlässigkeit im ungesättigten Bereich [-]
Q: Wassermenge, z.B. in [m³/s]
Ss: spezifischer Speicherkoeffizient
x,y: Koordinaten, z.B. in [m]
Der spezifische Speicherkoeffizient Ss ist definiert als die Änderung des gespeicherten Wasservolumens je Volumeneinheit des Grundwasserraums bei Änderung der Druckhöhe H bzw. bei Absenkung um einen Meter Wassersäule.
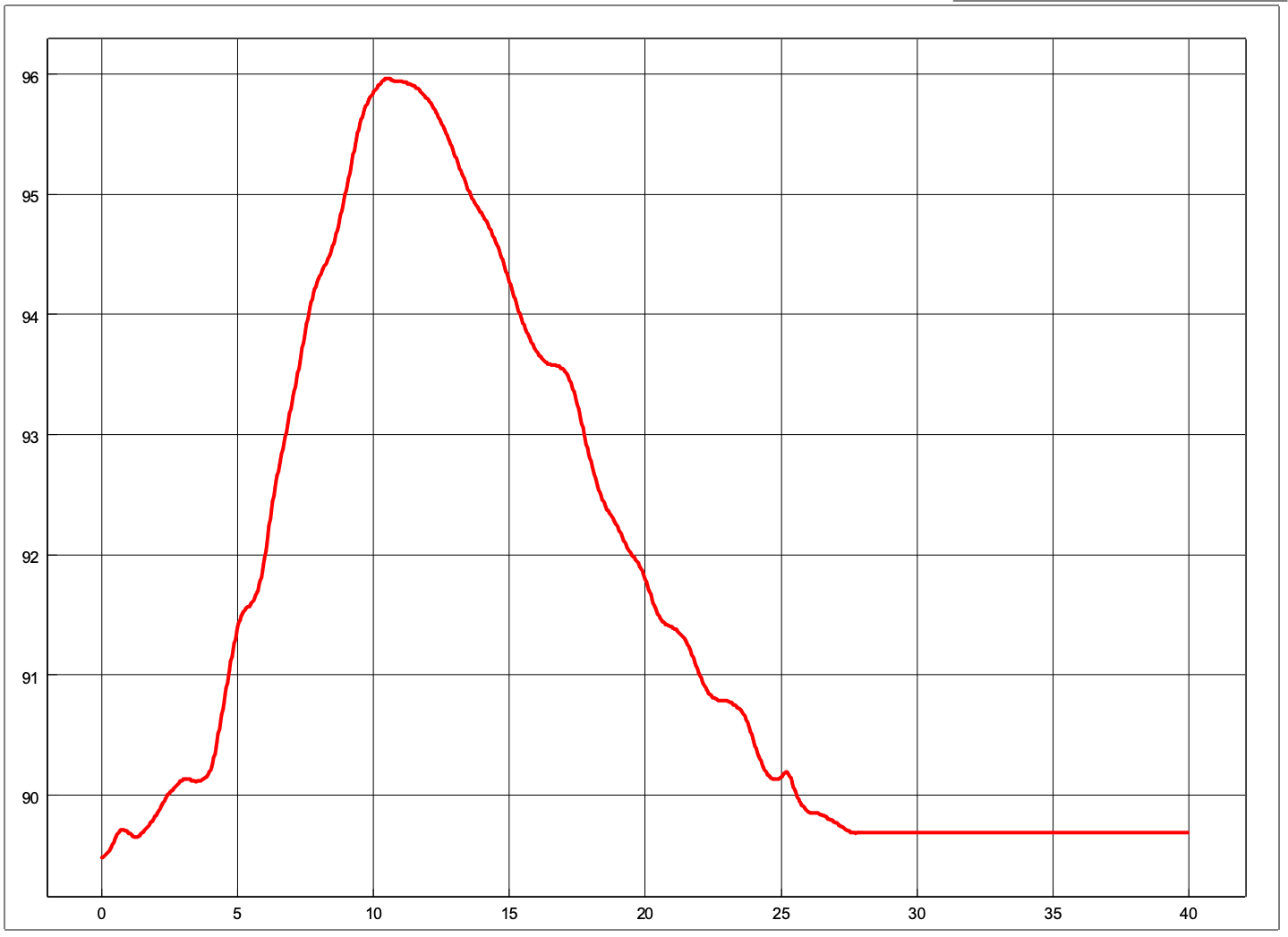
Es können im Programm GGU-2D-TRANSIENT Randbedingungen zeitabhängig definiert werden, u.a. als Randpotential, zeitabhängig, als Polygonzug z.B. einer auflaufenden Hochwasserwelle:
Diese Polygonzüge können einzelnen oder mehreren Systemknoten zugewiesen werden.
6.1 Auswertung der Berechnungsergebnisse der Grundwasserströmung
Die Auswertung und Darstellung der instationären Grundwasserströmungen wird mit dem Auswerteprogramm GGU-PLGW durchgeführt:
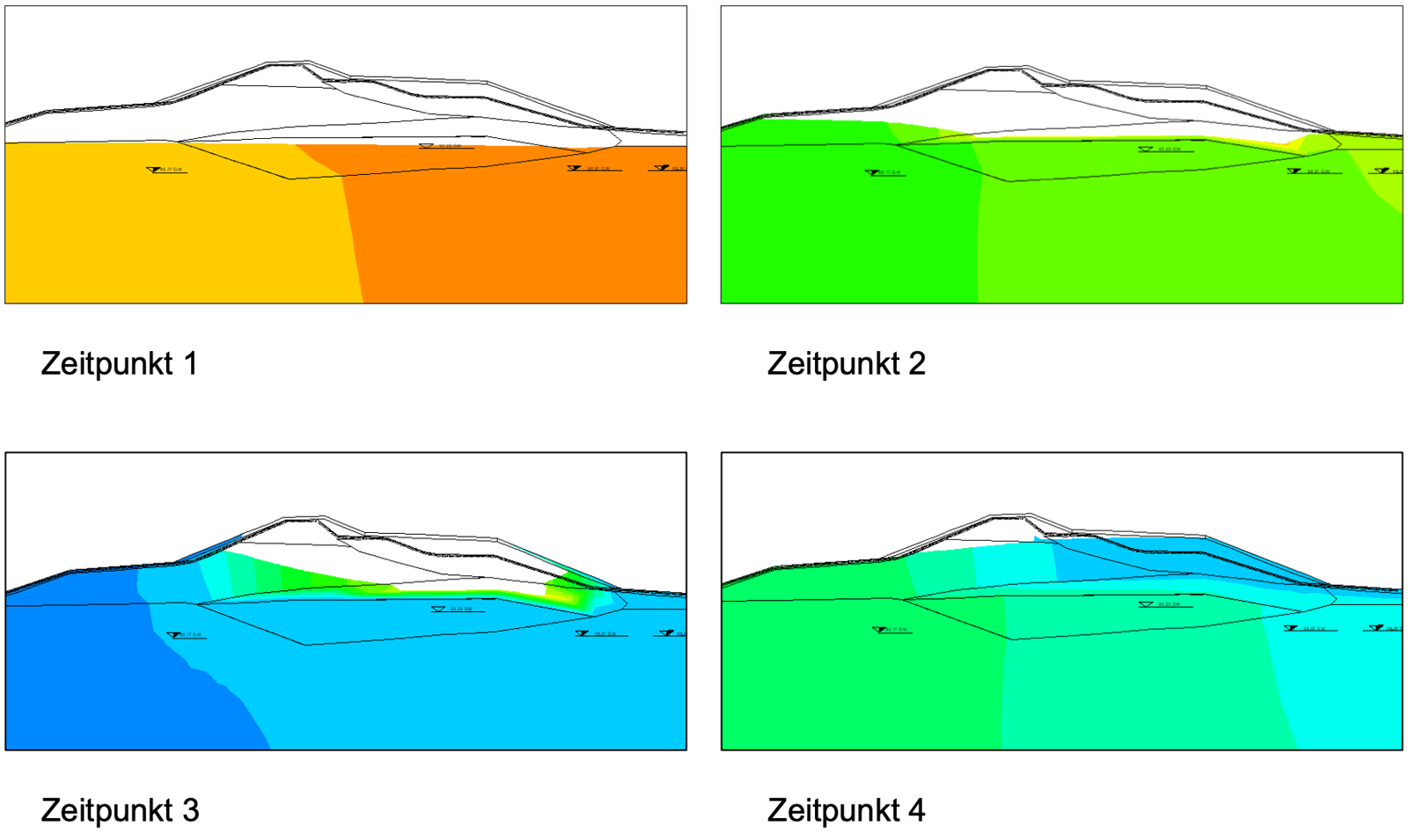
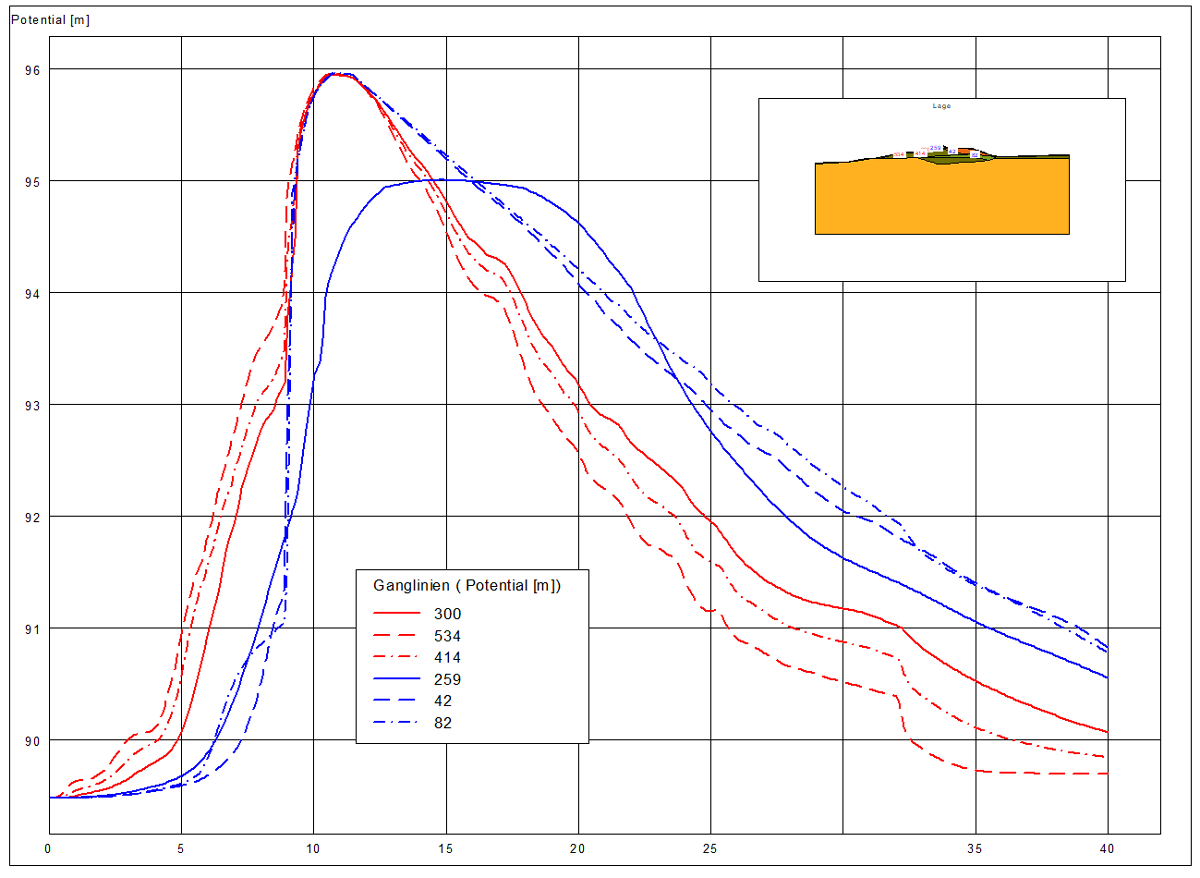
- Darstellung der verschiedenen Strömungsgrößen entlang von Schnitten durch das berechnete System
- z.B. ein farbiger Zeichentrick, der die Potentiale in bestimmten Zeitschritten wiedergibt
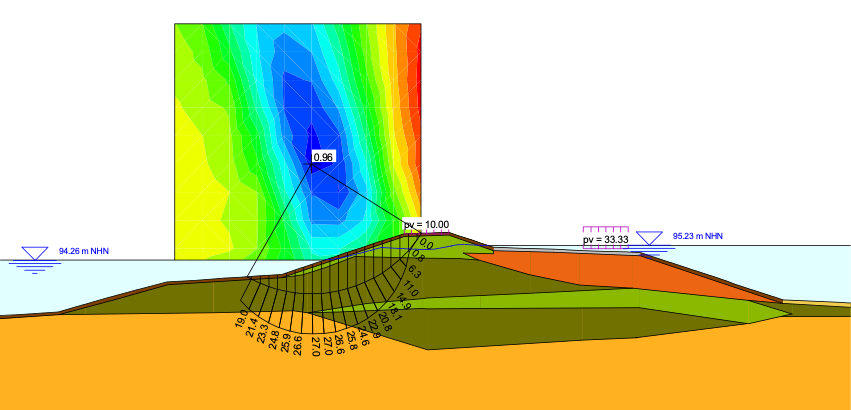
- Auslesen des Porenwasserdrucknetzes entlang von Schnitten durch das berechnete System für gewählte Zeitschritte als Grundlage von Standsicherheitsuntersuchungen mit GGU-STABILITY
7. Berechnungssystematik für zweidimensionale, vertikal ebene Probleme
7.1 Problemstellung stationär
- Untergrundhydraulische Untersuchungen mit Berechnung eines Porenwasserdrucknetzes mit GGU-2D-SSFLOW
- Auswertung (GGU-2D-SSFLOW)
7.2 Problemstellung instationär
- Untergrundhydraulische Untersuchungen mit Berechnung eines Porenwasserdrucknetzes für einen stationären Ausgangszustand mit GGU-2D-SSFLOW
- Auslesen der Grunddaten für die Berechnung mit GGU-2D-TRANSIENT
- Erstellen von Polygonzügen, z.B. für instationäre Potentialrandbedingungen
- Instationäre Berechnung mit GGU-2D-TRANSIENT
- Auswertung mit GGU-PLGW
8. Video zur Berechnung der Grundwasserströmungen
In diesem Video wird die instationäre untergrundhydraulische Berechnung eines Deichsystems mit flussseitiger Hochwasserwelle vorgeführt.
Hinweise zur Nutzung
Alle hier aufgeführten Texte, Bilder und Medien unterliegen dem Urheberrecht und sind geistiges Eigentum der Civilserve GmbH. Verwendung ist nur mit entsprechendem Hinweis und einer Verlinkung auf diese Quelle erlaubt.