Terzaghi’s consolidation theory
Table of content
1. Consolidation
Cohesive soils react with delayed settlements which depend on the grain composition and the water content. The settlements in soil layers consist of three components:
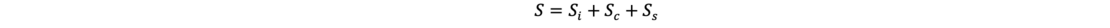
Si are settlements that occur immediately and do not involve any changes in the volume of the soil. The soil deflects laterally under the load. This is often referred to as elastic settlement.
Sc is called consolidation settlement. It is associated with a volume change in the soil. The water present in the cohesive soil is squeezed out and the soil adopts a higher density. Due to the very low water permeability of cohesive soils, no equilibrium in grain-to-grain pressure can be established immediately after loading, but in the process of water squeezing out, this equilibrium will be established as the water content decreases. With time, therefore, the excess pore water pressure created by the loading will be reduced. The settlements are thus established by the reduction of the excess pore water pressure. Sc is also referred to as primary settlement. In non-cohesive soils, the primary settlements occur at time t = 0 because of the high permeability.
Secondary settlements Ss are caused by creep processes in the soil, and are caused by long-lasting viscous flow phenomena of the grain structure. In the time-settlement diagram, the secondary settlements can be seen to grow steadily after the primary settlements. The time-settlement line therefore does not asymptotically approach a horizontal line.
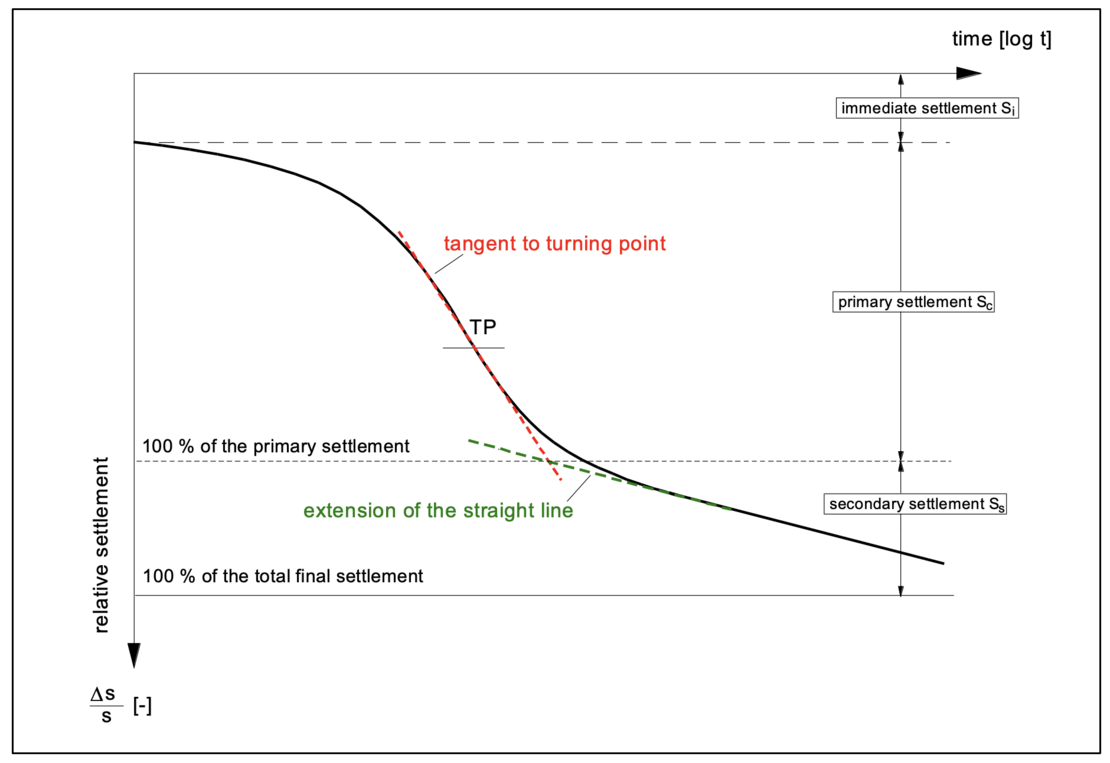
Immediately after the immediate settlement Si (t = 0) the consolidation process starts, the consolidation settlements Sc grow. The transition from primary and secondary settlements is defined - in the logarithmic scale – by the intersection of the tangent to the turning point of the time-settlement line for the primary settlement and the extension of the straight line describing the secondary settlements as shown in the following figure.
According to Terzaghi (1923), the differential equation describing a one-dimensional consolidation process is:
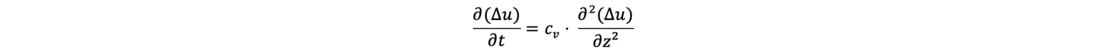
This equation is a partial linear and homogeneous differential equation of 2nd order. The term cv is the so-called coefficient of consolidation. With the permeability of the soil kf, the dead weight of the water γw and the constrained modulus Es, it results in:
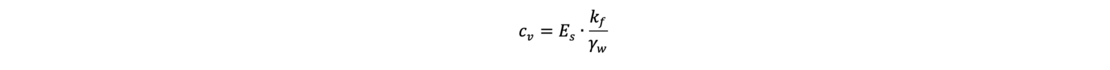
A Bernoulli product approach is used to solve this differential equation where φ(t) is a function dependent on time only and ψ(z) is a function dependent on depth only.
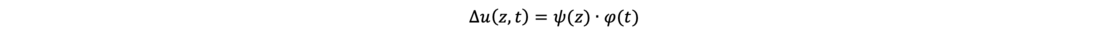
This splits the partial differential equation into two ordinary differential equations. For the solution an initial condition (isochrone at t = 0) and two homogeneous boundary conditions (drainage conditions) are needed. After some transformations two ordinary differential equations are obtained
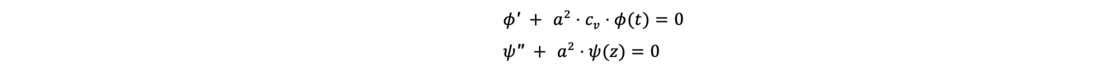
which have the following solutions:
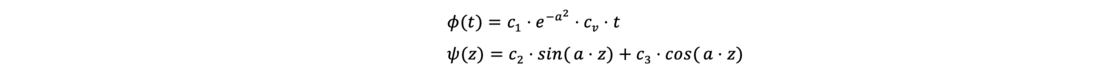
For the solution, the dewatering boundary conditions must be incorporated into these equations so that the constants C1 to C3 can be determined. With the resulting equations for the excess pore water pressure Δu as a function of time and depth z, isochrones can be calculated for various initial and boundary conditions. They are available as graphs in many standard textbooks.
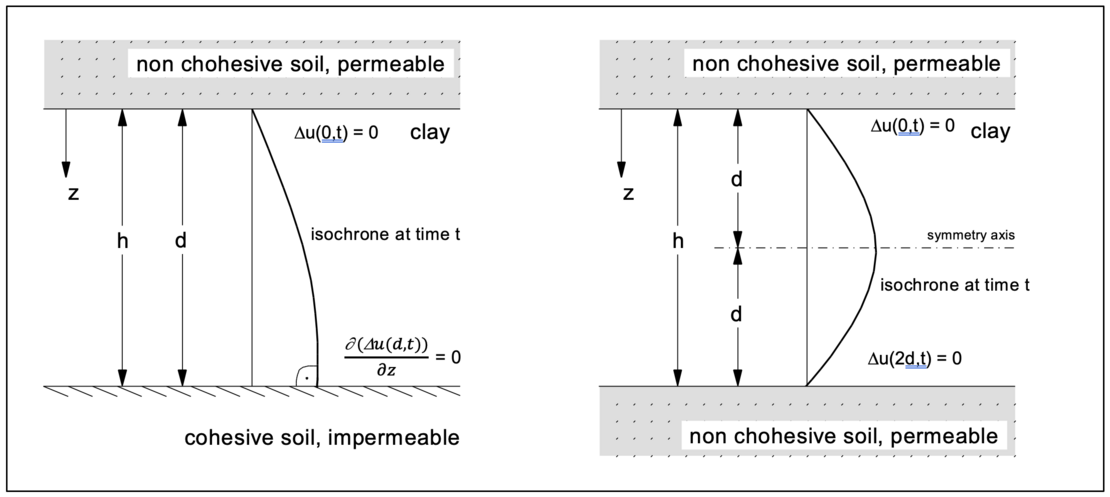
The boundary conditions are to be set up as a function of the water permeability of the soil flanking the layer to be drained. Non-cohesive soils represent a permeable boundary, the excess pore water pressures can dissipate there at times t > 0 after loading. Cohesive soils and rock form an impermeable boundary, the pore water cannot flow out there.
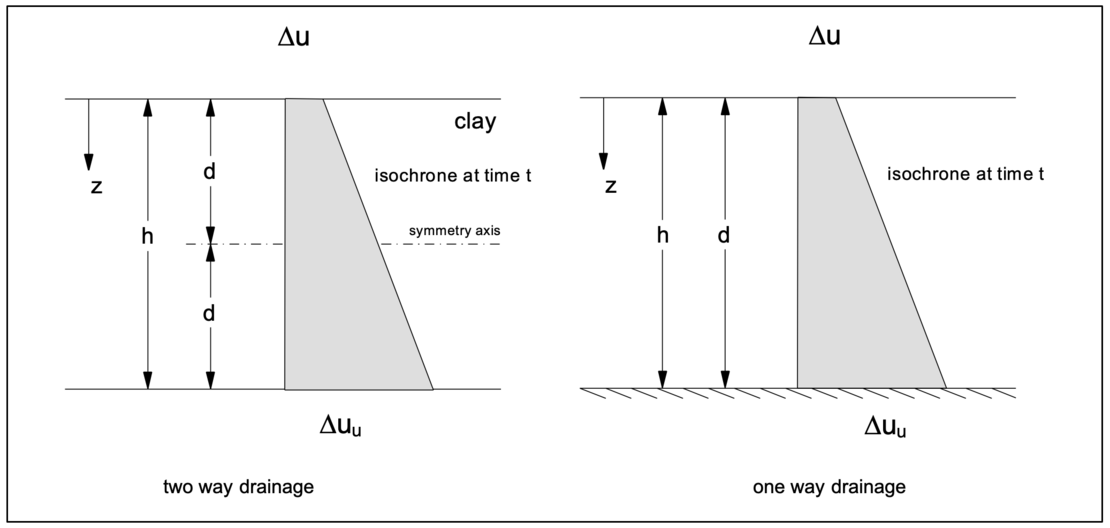
The following sketches show boundary conditions for a one way drainage (left) and for a two way drainage (right). By definition, the thickness of the layer to be consolidated is given as h = d for a one way drainage and h = 2 d for a two way drainage. Furthermore the isochrones for a uniform, constant load at time t > 0 are shown also.
After incorporating the initial conditions, the following equations are obtained as the final solution of the differential equation describing the development of the excess pore water pressure.
For the case of a uniform infinite surface load p on a layer to be consolidated (layer thickness h = 2 • d) for a two way drainage, the solution of the differential equation with T as a dimensionless time factor is:
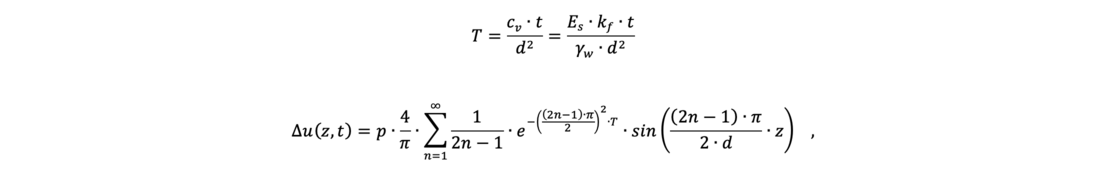
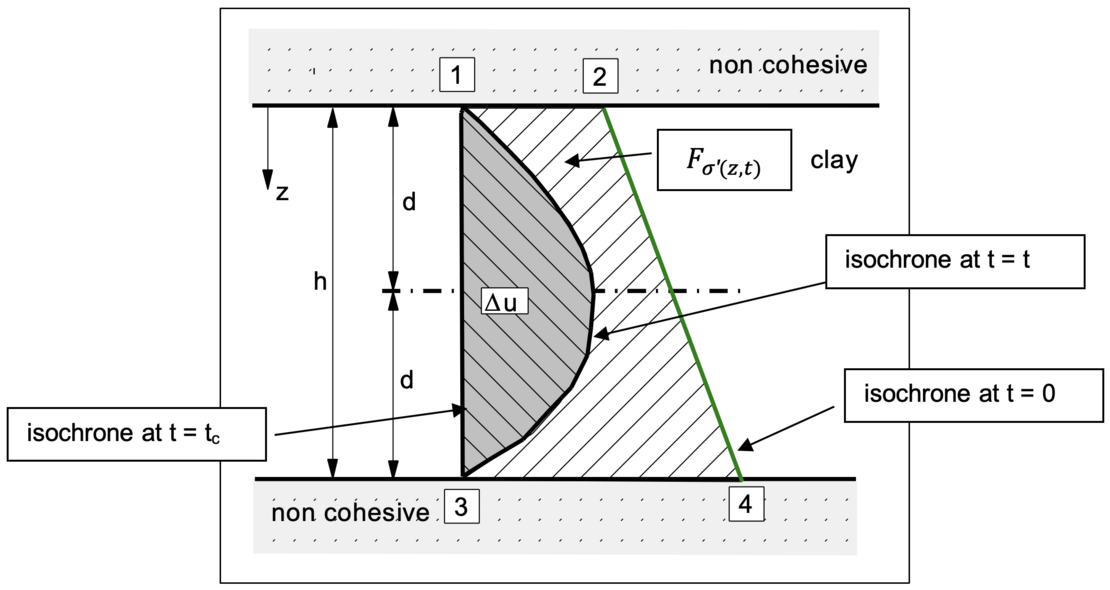
By definition, the value "d" describes half the height of the soil layer to be consolidated, see the figure below.
In case of a uniform infinite surface load p on a layer to be consolidated (layer thickness h = d) with a one way drainage, the solution of the differential equation is identical, but it should be noted that the value "d" describes the entire height of the soil layer to be consolidated by definition.
For a limited surface load with the resulting excess pore water pressure at time t = 0, the solutions of the differential equations are as follows for a layer to be dewatered with a two way drainage (layer thickness h = 2 • d) or one way drainage (layer thickness h = d) with the excess pore water pressure at the upper edge Δuo and at the lower edge Δuu at time t = 0:
- two way drainage („d“ represents half of the thickness of the soil layer):
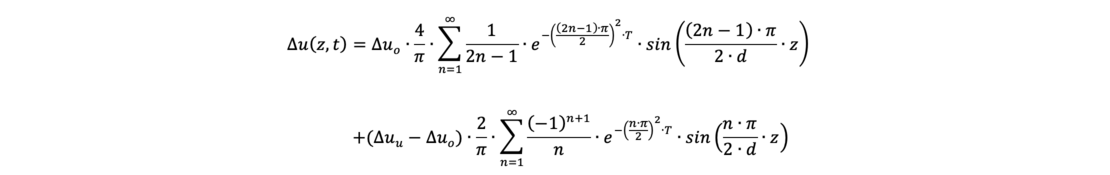
- one way drainage („d“ represents the thickness of the soil layer):
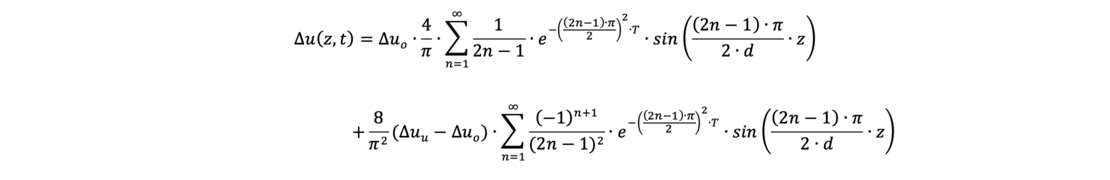
2. Degree of consolidation
The primary settlement of a cohesive soil s(t) results from the volume of water squeezed out. It tends towards a limit value s(t = ∞) which represents the maximum value or the final settlement. Their ratio is called the degree of consolidation uk.
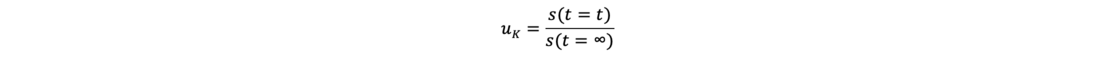
The effective stress σ‘ acts as the settlement-generating stress in a soil layer at a time t. The neutral stress u at time t is composed of the hydrostatic pore water pressure u0 and the excess pore water pressure Δu, whereby only the excess pore water pressure Δu is decisive for the consolidation theory. Thus, the following applies to the consolidation calculations
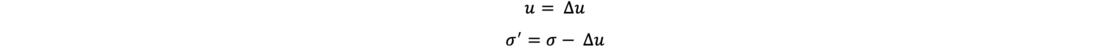
By integrating the settlement-generating - effective - stresses, divided by the constrained modulus, the settlement of a soil layer is obtained. The final settlement can be determined:
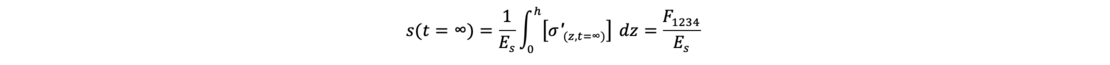
For a considered time t, the effective stresses can be calculated with
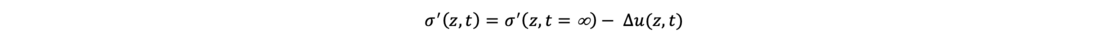
The corresponding settlements are
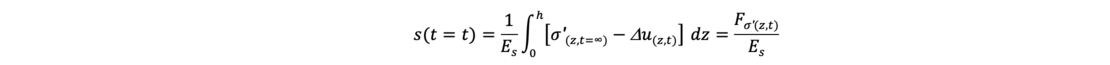
The degree of consolidation uk is thus given by
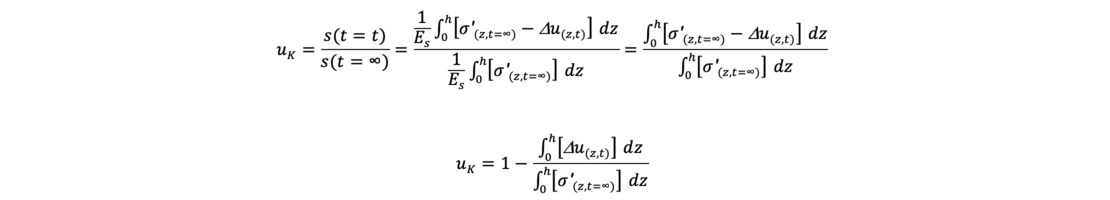
The degree of consolidation uk is the ratio of the hatched area Fσ‘(z,t) (= effective stresses at time t) to the total load area F1234 as effective stress at time t = ∞. As an example, the distribution of effective stresses and excess pore water pressure is shown here for a clay layer to be consolidated for a two way drainage.
The degree of consolidation uk can be calculated as a function of time t for a two way drainage with a linear isochrone at time t = 0
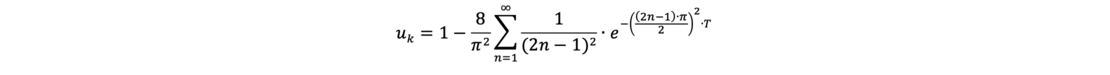
and for a one way drainage with
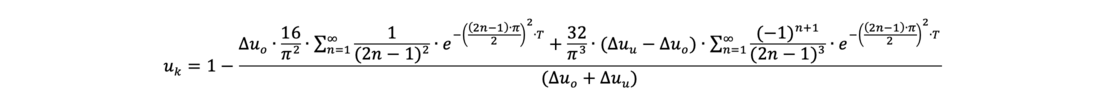
For different initial conditions described by the isochrone at time t = 0, the above equation can be simplified:
Δuo = Δuu: constant pore water pressure distribution over the soil layer to be drained
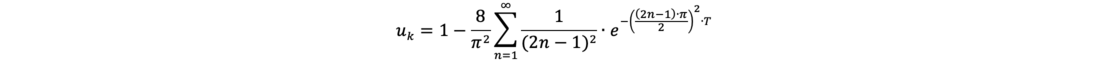
Δuo = 0: pore water pressure distribution increasing linearly with depth over the soil layer to be consolidated
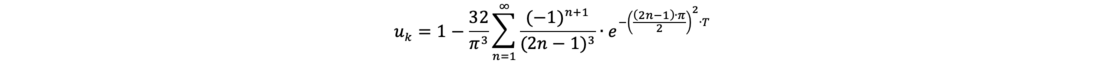
Δuu = 0: linear with depth, decreasing to zero pore water pressure over the soil layer to be consolidated
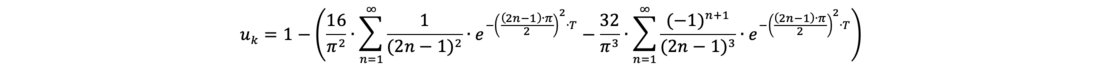
3. Example of the use of the computer program
For the example shown of an 8 m thick clay layer loaded with an unlimited surface load of p = 25 kN/m², the time for a degree of consolidation of Uk = 85 % and the corresponding settlement of the ground surface are to be determined in accordance with the one-dimensional consolidation theory using the computer program GGU-CONSOLIDATE.
Notes on use
All texts, images and media listed here are subject to copyright and are the intellectual property of Civilserve GmbH. Use is only permitted with appropriate reference and a link to this source.